Die Determinante von A läßt sich auch über die algebraischen Komplemente Ank ermitteln:
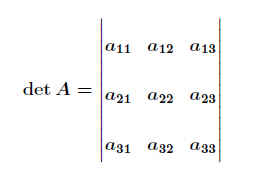 .
. .
Der Laplace’scher Entwicklungssatz ermöglicht die Berechnung der Determinante von Matrizen mit mehr als 3*3 Elementen.
Streicht man bei einer Determinante D die i-te Zeile und k-te Spalte, so heißt die verbliebene Determinante Unterdeterminante. Sie wird durch das Symbol Dik gekennzeichnet.
Die mit dem Vorzeichenfaktor (−1)i+k versehene Unterdeterminante Dik wird als algebraisches Komplement Aik bezeichnet.
Aik = (−1)i+k · Dik
Man kann sich das Vorzeichen entsprechend einem Schachbrettmuster vorstellen:
| + | − | + |
| − | + | − |
| + | − | + |
Die Determinante von A läßt sich auch über die algebraischen Komplemente Ank ermitteln:
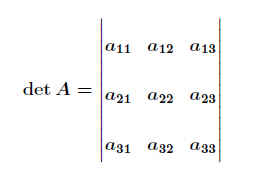 .
.
.
| = | a11 · a22 · a33 + a12 · a23 · a31 + a13 · a21 · a32 | − | |
| − | a13 · a22 · a31 − a11 · a23 · a32 − a12 · a21 · a33 | = | |
| = | a11 · ( a22 · a33 − a23 · a32) | − a12 · ( a21 · a33 − a23 · a31) | + a13 · (a21 · a32 − a22 · a31) |
| D11 | D12 | D13 | |
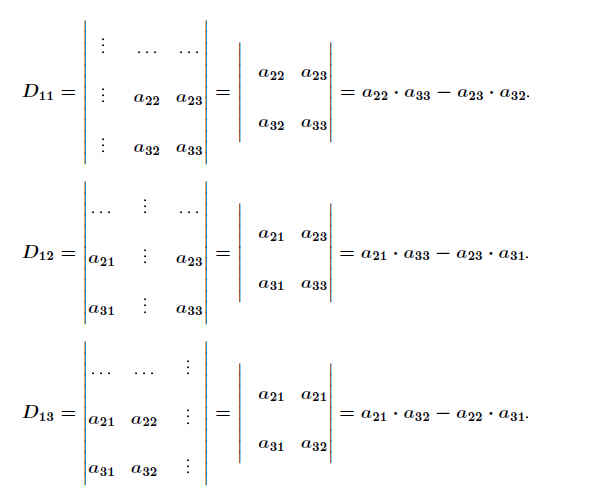 .
.
.
Damit kann man die Determinante D in der Form
D = a11D11 − a12D12 +a13D13 bzw.
D = a11A11 + a12A12 +a13D13 = ∑k=13 a1k · A1k
schreiben.
Allgemein kann man nach dem Laplaceschen Entwicklungssatz die Determinante einer 3x3-Matrix durch Entwickeln nach einer Zeile oder Spalte berechnen:
D = ∑k=13 aik · Aik oder
D = ∑i=13 aik · Aik .
Die Aik sind die algebraischen Komplemente von aik in D:
Aik = (−1)i+k · Dik .
.
Beispiel 16 - 29
mt9016 .
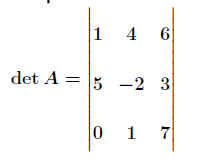 .
.
.
.
Lösung ansehen .
.