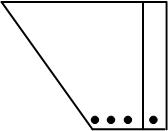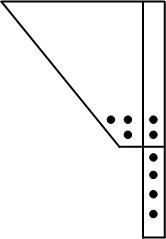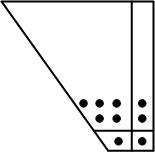
16.2.11  Lösungsverhalten eines linearen (m,n)-Gleichungssystems

Das Lösungsverhalten eines linearen (m,n)-Gleichungssystems wird durch die Homogenität/Inhomogenität des Gleichungssystems entscheidend geprägt:

1. Inhomogenes lineares Gleichungssystem A · x^→ = c^→
   Das System besitzt entweder genau eine Lösung oder unendlich viele Lösungen oder überhaupt keine Lösung.
2. Homogenes lineares Gleichungssystem A · x^→ = 0^→
   Das System besitzt entweder genau eine Lösung, nämlich die triviale Lösung x^→ = 0, oder unendlich viele Lösungen (darunter die triviale Lösung).

Ein gegebenes Gleichungssystem

kann man durch äquivalente Umformungen in ein gestaffeltes Gleichungssystem der Form

überführen.

---

Abbildung 86: eine / unendlich viele / keine Lösungen

---

.
In Matrixschreibweise :
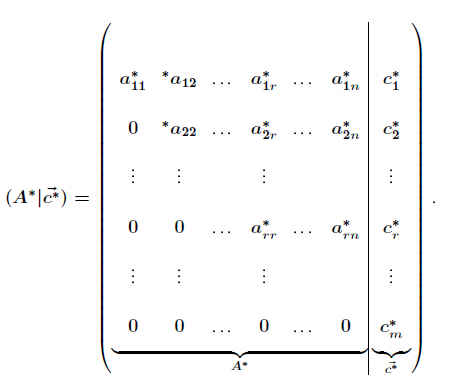
A · x^→ = c^→ wird durch äquivalente Umformungen in A^* · x^*→ = c^*→ überführt.
.
.
.
.

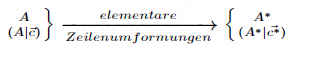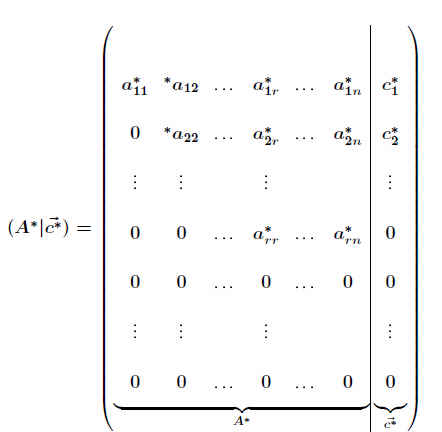
Damit das Gleichungssystem lösbar ist, muss die erweiterte Koeffizientenmatrix (A^* | c^*→) die spezielle Form

.
.
annehmen.
Sowohl die Matrizen a^* als auch (A^* | c^*→ ) sind von trapezförmiger Gestalt und enthalten in den letzten (m-r) Zeilen nur Nullen. Sie stimmen daher mit ihrem Rang überein:

Rg(A^*) = Rg(A^*|c^*) =r.

Da die erweiterten Matrizen (A|c) und (A^*|c^*) durch äquivalente Umformungen / elementare Zeilenumformungen ineinander übergegangen sind, sind die korrespondierenden Matrizen ebenso ranggleich. Dann gilt jedoch:

Ein lineares (m,n)-System A · c^→ = c^→ ist nur dann lösbar, wenn der Rang der Koeffizientenmatric A mit dem Rang der erweiterten Koeffizientenmatrix (A|c) übereinstimmt:

Rg (A) = Rg(A|c) = r     (r ≤ m ; r ≤ n)

Fallunterscheidungen

1. Fall: r = n
   Das gestaffelte System A^·x^→ = c^*→ besitzt für r =n die quadratische Form:
   

   a11*· x1	+ a12*· x2	+ …	+ a1n*· xn	=	c1*
   	+ a22*· x2	+ …	+ a2n*· xn	=	c2*
   			⋮		⋮
   			ann*· xn	=	cn*

   
   .
   
   In Matrixschreibweise :
   .
   .
   
   Nun kann man durch Rückwärtseinsetzen die Werte für x^→ bestimmen. Das Gleichungssystem besitzt genau eine Lösung
2. Fall: r < n
   Das gestaffelte System A^* · x^→ = c^*→ hat rechteckige Gestalt für r < n
   
   

   a11*· x1	+ a12*· x2	+ …	+ a1r*· xr	⋯	+ a1n*· xn	=	c1*
   	+ a22*· x2	+ …	+ a2r*· xr	⋯	+ a2n*· xn	=	c2*
   			⋮	⋮			⋮
   			arr*· xr	⋯	+ arn*· xn	=	cr*

   
   Damit haben wir mehr Unbekannte als Gleichungen: n > r. Davon sind n−r der Unbekannten, z.B. x_r+1, x_r+2, ⋯, x_n frei wählbare Größen (Parameter).
   Durch Rückwärtseinsetzen erhält man die unendlich vielen Lösungen des gestaffelten Systems, die dann durch die Parameter ausgedrückt werden.

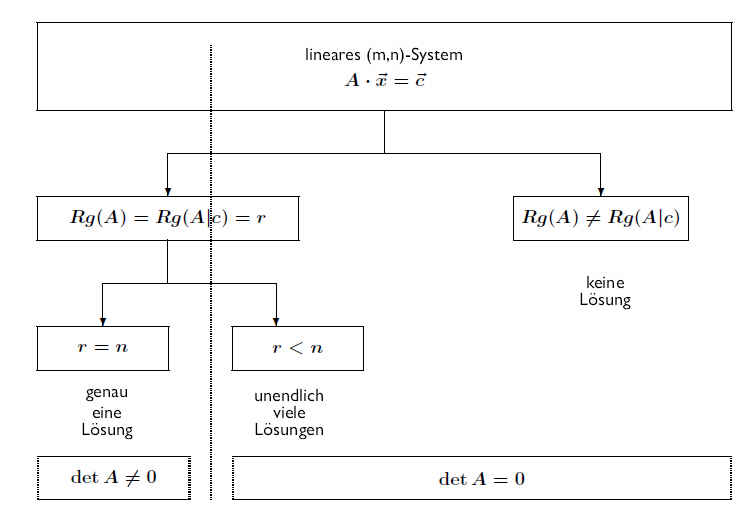
Zusammenfassung: Ein Lineares Gleichungssystem ist nur lösbar, wenn Koeffzientematrix A und erweiterte Matrix (A|c) ranggleich sind:

Rg (A) = Rg(A|c) = r

Im Falle der Lösbarkeit besitzt das lineare Gleichungssystem die folgende Lösungsmenge:
Für r = n : Genau eine Lösung
Für r < n : Unendlich viele Lösungen

In einem homogenen System A · x^→ = 0^→ ist die Lösbarkeitsbedingung Rg (A) = Rg(A|c) stets erfüllt. .
.
Beispiel 16 - 39 mt9023
Das Gleichungssystem

.
.

Lösung ansehen .
.

.
.
Beispiel 16 - 40 mt9024 .
Das Gleichungssystem

hat genau eine Lösung: .
.
Lösung ansehen .
.

.
.
Beispiel 16 - 41 mt9029 .
Das Gleichungssystem

.
ist lösbar und hat unendlich viele Lösungen: .
.
Lösung ansehen .
.