Setzt man in der Binomialverteilung .
.
.
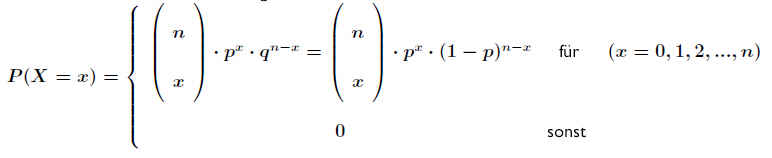den als sehr klein angenommenen Wert np=λ und läßt bei festem λ den Wert n beliebig wachsen (n → ∞ ), so geht die Binomialverteilung mit dem Erwartungswert np=λ in die Poissonverteilung über: .
.
.
x ist die Anzahl der Ereignisse, der Erwartungswert der Zufallsvariablen. .
Die Poissonverteilung kann statt der Binomialverteilung eingesetzt werden, wenn die Bedingungen
λ< 10 und n > 1500 · p erfüllt sind. .
Abbildung 95: Wahrscheinlichkeitsfunktion der Poisson-Verteilung für λ = 1
Der Funktionsaufruf hier ist: =POISSON.VERT(<x>;<lambda>;FALSCH). .
Beispiel 18 - 14 st9043
In einer Fabrik werden Teile mit 1 % Ausschuss hergestellt. In einer Zufallsstichprobe werden n=100 Teile entnommen. Wie groß ist die Wahrscheinlichkeit, 3 oder mehr schlechte Teile in der Stichprobe zu erhalten ?
.
Lösung ansehen .
.
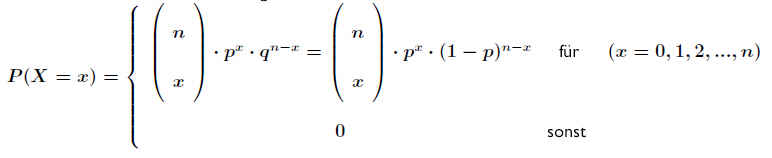