18.5.3 Binomialverteilung
Gegeben sei eine Urne mit schwarzen und weißen Kugeln. Bei jeder Ziehung wird die Nummer der Kugel festgehalten und sie danach zurückgelegt (’ Bernoulli-Experiment ’). Die Wahrscheinlichkeit, bei einer Ziehung eine weiße Kugel zu erhalten, sei p und ist wegen des Zurücklegens konstant. Dann ist q = 1−p die Wahrscheinlichkeit, eine schwarze Kugel zu ziehen. Die Anzahl der Permutationen ist demnach .
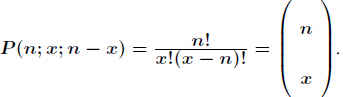 .
.
.
Die Wahrscheinlichkeit für die einzelnen Realisierungen ist damit .
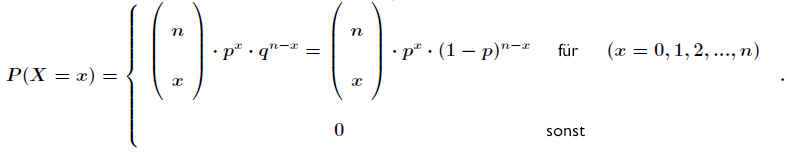 .
.
.
.
Trägt man nun für eine vorgegebene Anzahl von Kugeln und gegebenes p die Wahrscheinlichkeit auf, 1; 2; 3; ... n weiße Kugeln zu ziehen, erhält man die Wahrscheinlichkeitsfunktion. .
Eine einfache Realisierung (anstatt manuell auszumultiplizieren oder in einer Tabelle zu suchen) liefert z.B. eine Tabellenkalkulation für die einzelne Wahrscheinlichkeit: .
.
BINOM.VERT(Zahl_Erfolge;Versuche;Erfolgswahrsch;Kumuliert) .
.
Zahl_Erfolge entspricht x (’Laufvariable’) .
Versuche: Vorgegebene Zahl der Versuche = n .
Erfolgswahrsch: entspricht p .
Kumuliert: FALSCH - Wahrscheinlichkeitsfunktion , WAHR - Verteilungsfunktion .
Reiht man die Laufvariable in einer Spalte auf, so kann man mittels der Formel .
=BINOM.VERT(A1;6;0,1;FALSCH) .
die zugehörigen Werte in einer zweiten Spalte aufreihen und graphisch darstellen: .

| Abbildung 90: Binomialverteilung für n=6, p=0,1 |
.

| Abbildung 91: Binomialverteilung für n=6, p=0,5 |
.

| Abbildung 92: Binomialverteilung für n=6, p=0,8 |
Trägt man die Verteilungsfunktion auf, so kann man die Wahrscheinlichkeit ablesen, mindestens n Realisierungen nach x Versuchen zu erzielen: .

| Abbildung 93: Verteilungsfunktion der Binomialverteilung für n=6, p=0,8 |
Dies macht man sich zunutze bei Annahme-Stichprobenprüfungen. .
Beispiel 18 - 13 st9042
In einer Fabrik werden Teile mit 1,5 % Ausschuss hergestellt. Wie wahrscheinlich ist es, aus einer großen Lieferung in einer Zufallsstichprobe mit 5 entnommenen Teilen genau 0,1,2,3,4 bzw. 5 fehlerhafte Stücke zu finden ?
Tabelle der Wahrscheinlichkeitsfunktion: .
| x | 0 | 1 | 2 | 3 | 4 | 5 |
| P(X=x) | 0,92722 | 0,07060 | 0,00215 | 0,00003 | 0,00000 | 0,00000 |
| P(X=x) | 92,72 % | 7,06 % | 0,22 % | 0,00 % | 0,00 % | 0,00 % |
|
.
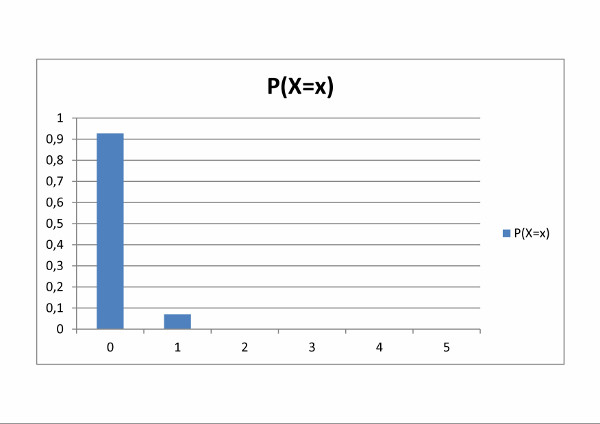
| Abbildung 94: Stichprobe für n=5, p=0,15 |
.
.
Lösung ansehen .
.
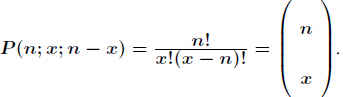 .
. 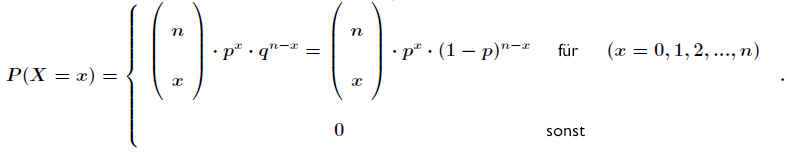 .
. 



