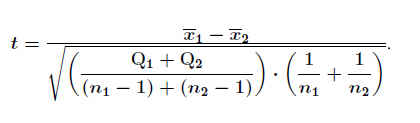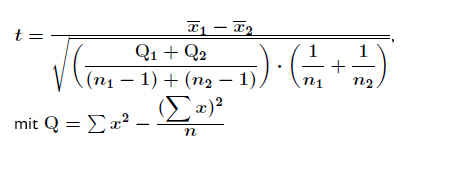19.1.6 t-Test für zwei (ungepaarte) Stichproben
.
Eine häufige Anwendung ist der t-Test für zwei Stichproben als ’Vergleich von Mittelwerten’. Es werden zwei Stichproben miteinander verglichen, die normalverteilt sein müssen. .
Setzt man weiterhin unabhängige Stichprobenmittelwerte mit gleicher, aber unbekannter Standardabweichung voraus, so kann man für die Prüfgröße t angeben: .
 .
.
.
mit : .
x1 := arithmetisches Mittel von Stichprobe 1 .
x2 := arithmetisches Mittel von Sti chprobe 2 .
∑x12 := Summe über die quadrierten Elemente aus Stichprobe 1 .
∑x22 := Summe über die quadrierten Elemente aus Stichprobe 2 .
(∑x1)2 := Quadrat der Summe über die Elemente aus Stichprobe 1 .
(∑x2)2 := Quadrat der Summe über die Elemente aus Stichprobe 2 .
n1 := Anzahl der Elemente in Stichprobe 1 .
n2 := Anzahl der Elemente in Stichprobe 2. .
.
Die Anzahl der Freiheitsgrade ν ist die Anzahl der freien Klassen und erechnet sich wie folgt: .
ν = (n1 − 1) + (n2 − 1). .
Führt man die Hilfsvariable
Q = ∑x2 − (∑x)2 / n ein, so wird der Ausdruck für t .
.
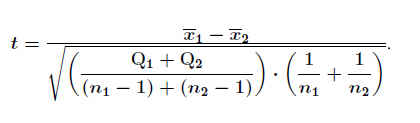 .
.
.
Beispiel 19 - 23 st9085
Eine Pharmafirma testet die Wirkung eines Wirkbeschleunigers auf Männer und Frauen. .
Gemessen wird die Dauer in Minuten, bis die Wirkung eintritt. Annahme ist, daß der Wirkbeschleuniger bei beiden Versuchsgruppen gleich gut wirkt. .
Der Wirkbeschleuniger wurde an 6 Männern und 8 Frauen getestet. .
Die Wirkungsdauern betragen: .
.
| Nr | Männer | Frauen . |
| 1 | 6 | 4,5 . |
| 2 | 9 | 12 . |
| 3 | 7,5 | 10,5 . |
| 4 | 6 | 9 . |
| 5 | 7,5 | 10,5 . |
| 6 | 9 | 9 . |
| 7 | | 10,5 . |
| 8 | | 9 . |
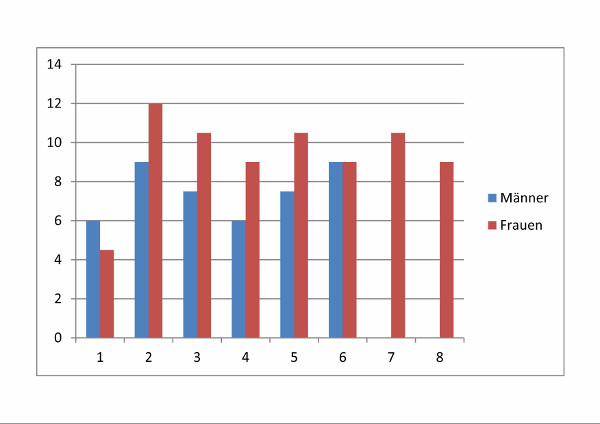
| Abbildung 103: Wirkungsdauer eines Wirkbeschleunigers |
.
Wirkt der Wirkbeschleuniger nun unterschiedlich oder nicht ? .
.
Nullhypothese (H0): .
Es gibt keinen Unterschied in der Wirkung des Wirkbeschleunigers auf Männer und Frauen. .
Alternativhypothese (H1): .
Der Wirkbeschleuniger wirkt bei Männern anders als bei Frauen, d.h. es gibt einen Unterschied. .
Wir gehen davon aus, daß die Stichproben normalverteilt sind und sich die Standardabweichungen nicht signifikant unterscheiden (eigentlich müßte das vor Durchführung des Tests noch überprüft werden). Das Vertrauensintervall wird auf 95% =0.95 festgelegt, damit ist a =0,05.
Die Stichproben sind unabhängig, damit kann man für die Prüfgröße t angeben: .
.
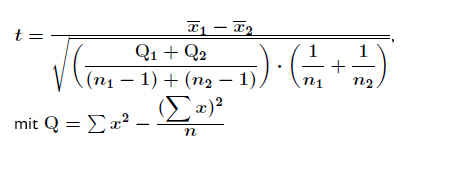 .
.
.
.
.
Das negative Vorzeichen bedeutet, daß Stichprobe 2 einen größeren Effekt hat als Stichprobe 1. .
Da es sich um einen zweiseitigen Test handelt, ergibt sich mit Hilfe von =T.INV.2S(0,95;12) oder =T.INV(0,975;12) ein Wert von t = 2,1788. .
Also ist der errechnete Wert t kleiner als der berechnete Wert und die Nullhypothese muß angenommen werden, d.h. es gibt keinen geschlechtsspezifischen Unterschied in der Wirkung des Wirkbeschleunigers. .
.
Lösung ansehen .
.
 .
.