19.2.1 Korrelationsmasse
Eine Vielzahl von Zusammenhängen wird lediglich vermutet, ohne dies zu belegen. Als Indiz für Zusammenhänge bedient man sich der Kenngrößen von Korrelationen wie den Korrelationskoeffizienten .
Es seien zwei Merkmale x und y zu beobachten. Bei einer Stichprobe im Umfang von n ergeben sich n Wertepaare (xi;yi) mit (i = 1, ..., n).
Beispiel 19 - 24: Fruchtbarkeitsrate
Es soll untersucht werden, ob das Bevölkerungswachstum eines Landes mit der Fruchtbarkeitsrate (durchschnittliche Zahl der Geburten einer gebärfähigen Frau) zusammenhängt. Es wurden acht Länder zufällig ausgewählt und wir erhalten die Daten .
.
| Land | Bevölkerungswachstum x | Fruchtbarkeitsrate y |
| Ägypten | 1,8 | 3 |
| Türkei | 1,1 | 2 |
| Vereinigte Arabische Emirate | 1,6 | 3 |
| Jamaika | 0,7 | 2 |
| Mauretanien | 2,9 | 5 |
| Island | 1 | 1,8 |
| Tadschikistan | 2,1 | 4,1 |
| Gabun | 2,4 | 4,7 |
(aus [de.wikibooks.org].)
.
Um einen Eindruck vom Zusammenhang der Daten zu erhalten, trägt man sie in einem Streudiagramm ab.
.
Als Masszahl für die Korrelation definiert man den Korrelationskoeffizienten so, daß er Werte zwischen -1 und 1 annehmen kann.
Ist der Korrelationskoeffizient bei +1 oder -1, so kann man von einem linearen Zusammenhang der beiden Datenreihen ausgehen. Liegt dieser Koeffizient bei Null, ist ein linearer Zusammenhang nicht zu vermuten.
Der Korrelationskoeffizient nach Bravais-Pearson ist definiert als .
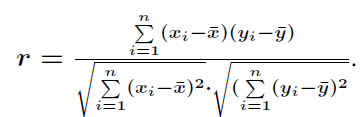 .
.
.
.
In Excel können die beiden (gleichen) Funktionen Korrel() oder Pearson() hierzu verwendet werden.
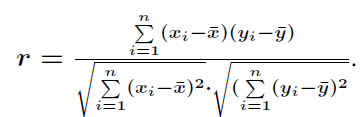 .
.