20.3.2  Regression mit einem Polynom zweiter Ordnung

Wir dehnen den o.a. Ansatz aus auf die Gleichung mit einer Parabel. .
Gesucht ist eine Kurve entsprechend einer Funktion y=ax² + bx + c, deren Summe der Abstandsquadrate (f(x_i) − y_i) in y-Richtung minimal wird: .
.
S = ∑_i=1ⁿ v_i² = ∑_i=1ⁿ (y_i−f(x_i))² = ∑_i=1ⁿ (y_i−ax² + bx + c)² → Minimum. .
.
Die Werte der Parameter werden wieder bestimmt über .
.
∂   S/ ∂ a = 0,   ∂   S/ ∂ b = 0   ∂   S/ ∂ c = 0 . .
.
Eingesetzt: .
.
∂   S/ ∂ a = 2 · ∑_i=1ⁿ (y_i − a x_i² −bx_i−c)· (−x_i²) = 0 .
.
∂   S/ ∂ b = 2 · ∑_i=1ⁿ (y_i − a x_i² −bx_i−c)· (−x_i) =0 .
.
∂   S/ ∂ c = 2 · ∑_i=1ⁿ (y_i − a x_i² −bx_i−c)· (−1) =0 .
.
Ausmultiplizieren und die Terme ohne Koeffizienten a,b,c auf die rechte Seite gebracht: .
.
.
.
.
.
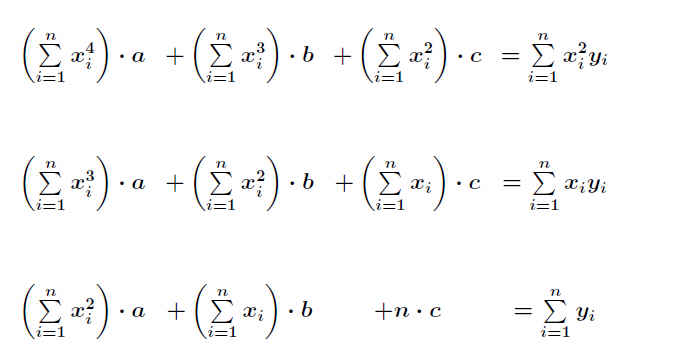Gelöst wird dieses Gleichungssystem mit den Standard-Methoden (z.B. Gauß, Gauß-Jordan). .
Beispiel 20 - 30 st9210
Für ein Fahrzeug soll der Zusammenhang zwischen der Geschwindigkeit v und dem Bremsweg s bestimmt werden. Fünf Messungen ergeben die Wertepaare : .
.

.
.
Wie lauten die Parameter der Ausgleichsparabel .
y=ax²+bx+c (x entspricht v_i, y entspricht s_i) ? .
.
.
Lösung ansehen .
.

.