SchreibweisenAuch wenn in der Mathematik viele Zusammenhänge und Schreibweisen eindeutig festgelegt sind, gibt es in einigen Fälle Variationsmöglichkeiten: - Vielfach wird, wenn Missverständnisse ausgeschlossen sind, der "Malpunkt" weggelassen, z. B. meinen
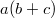 und und 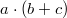 dasselbe. Bei dasselbe. Bei 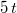 und und 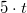 ist das ebenso. Auch kann der Faktor ist das ebenso. Auch kann der Faktor 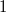 bei der Multiplikation weggelassen werden, z. B. ist bei der Multiplikation weggelassen werden, z. B. ist 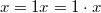 . Es ist in diesen Fällen natürlich nie falsch, den "Malpunkt" hinzuschreiben. . Es ist in diesen Fällen natürlich nie falsch, den "Malpunkt" hinzuschreiben.
- Bei Brüchen ist es unerheblich, ob man
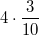 oder oder 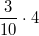 oder oder 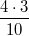 schreibt. Allerdings ist hier bei allen drei Schreibweisen der "Malpunkt" zwingend erforderlich, da schreibt. Allerdings ist hier bei allen drei Schreibweisen der "Malpunkt" zwingend erforderlich, da 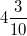 als als 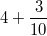 verstanden wird bzw. verstanden wird bzw. 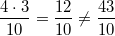 ist. ist.
- Bei Funktionen wie dem Sinus oder dem Logarithmus können die Klammern weggelassen werden, wenn keine Verwechslungsgefahr besteht. Es ist beispielsweise:
- U. a. in den folgenden Fällen sollten aber unbedingt Klammern gesetzt bzw. die Reihenfolge des Aufschreibens so gewählt werden, dass Missverständnisse ausgeschlossen sind, sonst können Verwechslungen auftreten:
-
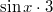 : Es könnte sowohl : Es könnte sowohl  als auch als auch 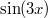 gemeint sein. gemeint sein. -
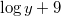 : Es könnte sowohl : Es könnte sowohl 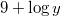 als auch als auch 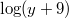 gemeint sein. gemeint sein.
Grundsätzliches zu KlammernKlammern sind in vielen Fällen unerlässlich, weil sie die Reihenfolge der Rechenoperationen ändern können. Es gilt: - Eine Klammer zu viel ist im Normalfall besser als eine Klammer zu wenig! Wenn Sie sich nicht sicher sind, schreiben Sie lieber Klammern hin.
- Verschachtelte Klammern werden von innen nach außen aufgelöst!
- Ein Bruchstrich wirkt wie eine Klammer - eine Klammer muss gesetzt werden, wenn der Bruchstrich durch : ersetzt wird bzw. wenn mehrere Brüche auf einem Bruchstrich zusammengefasst werden!
|
|
 Brückenkurs
Brückenkurs