ErklärungenAllgemeinesGrundlegende Definition einer Potenz: 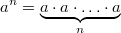 für 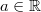 und 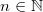 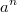 ist also erst mal nur eine abkürzende Schreibweise für ein Produkt mit vielen gleichen Faktoren.  heißt dabei Basis und 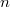 Exponent Exponent. Es gilt: -
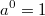 für für 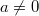
-
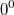 ist nicht definiert. ist nicht definiert.
-
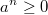 , wenn , wenn 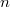 gerade ist gerade ist
Ganz wichtig: Im Allgemeinen ist 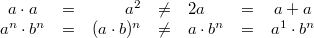 Außerdem gilt immer: Potenzrechnung geht vor Punktrechnung geht vor Strichrechnung! Auch hier können ausschließlich Klammern eine andere Reihenfolge der Rechenoperationen festlegen. Potenzen, Wurzeln und Logarithmen hängen sehr eng zusammen, nämlich: Das Rechnen mit Potenzen gibt Antwort auf die Frage: Welches Ergebnis erhalte ich, wenn ich die Zahl  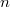 -mal mit sich selbst multipliziere? Das Rechnen mit Wurzeln gibt Antwort auf die Frage: Welche Zahl ergibt  , wenn ich sie 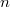 -mal mit sich selbst multipliziere? Formal geschrieben: ![a^n=x \Leftrightarrow a=\sqrt[n]{x}](./teximg/img802.png) Das Rechnen mit Logarithmen gibt Antwort auf die Frage: Wie oft muss ich die Zahl  mit sich selbst multiplizieren, damit das Ergebnis  ist? Formal geschrieben: 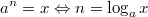 PotenzgesetzeBeim Rechnen mit Potenzen sind die fünf Potenzgesetze von großer Bedeutung. Sie können sowohl "von links nach rechts" als auch "von rechts nach links" gelesen werden - je nachdem, was sich für die entsprechende Aufgabe anbietet. 1. 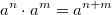 2. 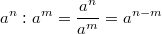 3. 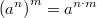 4. 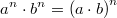 5. 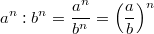 Die Potenzgesetze gelten für: 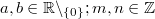 oder 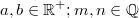 (für Erklärungen zu 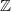 , 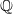 und 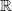 siehe Mengen u. a.). Das heißt, dass Potenzen nicht nur für natürliche Exponenten (wie bei der Definition oben) definiert sind, sondern auch negative bzw. gebrochene Exponenten möglich sind. Allerdings gibt es dann Einschränkungen bei den Basen. Insbesondere gelten folgende Festlegungen: -
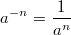 mit mit 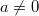
Bemerkung 1: Bei ![\sqrt [n]{a}](./teximg/img819.png) heißt 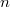 Wurzelexponent Wurzelexponent und  Radikand Radikand. Bemerkung 2: Solange keine Missverständnisse auftreten können, schreibt man 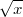 statt ![\sqrt[2] {x}](./teximg/img821.png) . Rechnen mit WurzelnDa Wurzeln als Potenzausdrücke mit gebrochenen Exponenten geschrieben werden können, gelten auch für Wurzeln die oben aufgeführten Potenzgesetze. In vielen Veröffentlichungen findet man spezielle Wurzelgesetze. Diese formulieren aber bloß die Potenzgesetze in Wurzelschreibweise. Daher verzichten wir hier darauf, zumal es sich auch sonst lohnt, mit dieser Schreibweise vertraut zu sein. U. a. erleichtert nämlich die Potenzschreibweise von Wurzel termen das Ableiten sehr. Darüberhinaus ist zu beachten: - Wurzeln sind immer nichtnegativ:
![\sqrt[n]{x} \geq 0](./teximg/img822.png) . Da beim Quadrieren möglicherweise Minuszeichen "verloren" gehen, muss beim Wurzelziehen aus quadratischen Termen also der Betrag des Ergebnisses betrachtet werden: . Da beim Quadrieren möglicherweise Minuszeichen "verloren" gehen, muss beim Wurzelziehen aus quadratischen Termen also der Betrag des Ergebnisses betrachtet werden: 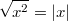
- Nach den Festlegungen oben darf der Radikand nicht negativ sein. Klassischerweise formuliert man: Im Bereich der reellen Zahlen dürfen aus negativen Zahlen keine Wurzeln gezogen werden! Allerdings sind Wurzeln aus negativen Zahlen dann erlaubt, wenn der Wurzelexponent ungerade ist: Ist
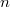 ungerade und ungerade und  negativ, gilt: negativ, gilt: ![\sqrt[n]{a}=-\sqrt[n]{\vert a \vert}](./teximg/img824.png) . Diese Umformung bewirkt aber gerade, dass unter der Wurzel wieder etwas Nichtnegatives steht. . Diese Umformung bewirkt aber gerade, dass unter der Wurzel wieder etwas Nichtnegatives steht.
- Aus Summen können keine Wurzeln gezogen werden! Anders formuliert: Wurzeln aus Summen lassen sich im Allgemeinen nicht vereinfachen, insbesondere ist:
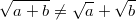 für fast alle für fast alle  und und  . Das können Sie prüfen, indem Sie auf beiden Seiten beliebige, von . Das können Sie prüfen, indem Sie auf beiden Seiten beliebige, von 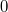 verschiedenen Zahlen einsetzen und die Ergebnisse vergleichen. verschiedenen Zahlen einsetzen und die Ergebnisse vergleichen.
Bemerkung: Im Bereich der natürlichen Zahlen sind Wurzeln aus Quadratzahlen, wie 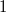 , 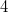 , 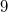 etc., wieder natürliche Zahlen; Wurzeln aus Nicht-Quadratzahlen, wie 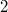 , 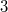 , 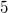 etc., sind irrationale Zahlen, d. h. sie sind unendliche, nichtperiodische Dezimalzahlen. Rechnen mit LogarithmenDer Logarithmus 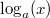 ist definiert für 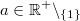 und 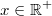 . Dabei heißt  Basis Basis und  Argument des Logarithmus' Argument des Logarithmus'. Die Basis muss nicht hingeschrieben werden, wenn die Umformung allgemein für alle Basen gilt oder wenn klar ist, um welche Basis es sich handelt. Warum gelten diese Einschränkungen für die Basis und das Argument? - Potenzen mit negativen Basen sind nur für ganzzahlige Exponenten definiert. Das heißt: Ein Term wie
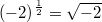 liefert kein Ergebnis. Genau dieses Ergebnis bräuchte der Logarithmus aber als Argument. liefert kein Ergebnis. Genau dieses Ergebnis bräuchte der Logarithmus aber als Argument. - Ein Potenzausdruck mit der Basis
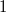 wäre eine ziemlich langweilige Angelegenheit, denn wäre eine ziemlich langweilige Angelegenheit, denn 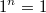 für alle für alle 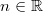 . Betrachtet man umgekehrt den Logarithmus, also die Frage, wie oft die Basis . Betrachtet man umgekehrt den Logarithmus, also die Frage, wie oft die Basis 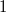 mit sich selbst multipliziert werden muss, damit das Ergebnis mit sich selbst multipliziert werden muss, damit das Ergebnis 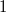 ist, gibt es darauf keine eindeutige Antwort. Da nicht eindeutige Antworten in der Mathematik (meist) nicht sinnvoll sind, schließt man ist, gibt es darauf keine eindeutige Antwort. Da nicht eindeutige Antworten in der Mathematik (meist) nicht sinnvoll sind, schließt man 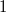 als Basis aus. als Basis aus.
- Setzt man voraus, dass die Basis positiv ist, kann das Ergebnis des Potenzausdrucks nie negativ oder
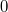 werden, denn für negative Exponenten gilt ja werden, denn für negative Exponenten gilt ja 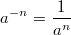 (siehe oben) und das ist in diesem Fall immer größer als (siehe oben) und das ist in diesem Fall immer größer als 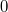 . Da der Logarithmus genau dieses Ergebnis als Argument verwendet, kommen also nur positive Argumente infrage. . Da der Logarithmus genau dieses Ergebnis als Argument verwendet, kommen also nur positive Argumente infrage.
Wichtig: Der Logarithmus selbst (also das "Ergebnis") kann trotz dieser Einschränkungen durchaus negativ oder nicht ganzzahlig sein. LogarithmengesetzeFür das Rechnen mit Logarithmen gelten die folgenden Logarithmengesetze, die sich direkt aus den Potenzgesetzen ableiten lassen: 1. 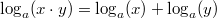 2. 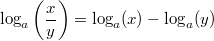 3. 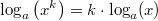 Die Logarithmengesetze gelten analog zur Logarithmusdefinition für 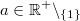 , 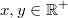 und 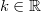 Weitere GesetzmäßigkeitenFür alle 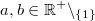 und 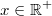 gilt: -
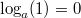 , denn , denn 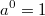 für alle Basen für alle Basen  , die hier betrachtet werden. , die hier betrachtet werden.
-
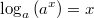 , denn Potenzen und Logarithmen sind Umkehroperationen. , denn Potenzen und Logarithmen sind Umkehroperationen.
-
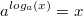 , denn Potenzen und Logarithmen sind Umkehroperationen. , denn Potenzen und Logarithmen sind Umkehroperationen.
-
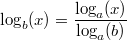 Diese Umrechnung ist als Basistransformation bekannt und wird z. B. benutzt, wenn Diese Umrechnung ist als Basistransformation bekannt und wird z. B. benutzt, wenn  eine ungewöhnliche Basis für den Logarithmus ist, die mithilfe des Taschenrechners nicht berechnet werden kann oder wenn in einer Rechnung mehrere Logarithmen mit unterschiedlichen Basen auftreten, die man zusammenfassen möchte. Diese Gleichung ermöglicht es, den Logarithmusterm so umzuformen, dass eine beliebige andere Zahl eine ungewöhnliche Basis für den Logarithmus ist, die mithilfe des Taschenrechners nicht berechnet werden kann oder wenn in einer Rechnung mehrere Logarithmen mit unterschiedlichen Basen auftreten, die man zusammenfassen möchte. Diese Gleichung ermöglicht es, den Logarithmusterm so umzuformen, dass eine beliebige andere Zahl  (mit den oben genannten Einschränkungen) als Basis auftritt. Bitte beachten Sie, dass (mit den oben genannten Einschränkungen) als Basis auftritt. Bitte beachten Sie, dass 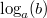 einfach eine Zahl ist. einfach eine Zahl ist.
NamenskonventionenEinige Logarithmen, die man besonders häufig braucht, haben spezielle Namen bekommen: - Zweierlogarithmus oder logarithmus dualis:
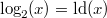
- Natürlicher Logarithmus oder logarithmus naturalis:
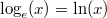
- Zehnerlogarithmus oder dekadischer Logarithmus:
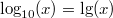
Anwendungen: Der Zweierlogarithmus wird u. a. in der Informatik für Rechnungen im Binärsystem verwendet. Der natürliche Logarithmus hängt eng mit Exponentialfunktionen und Zinsrechnung zusammen. Der Zehnerlogarithmus spielt beispielsweise bei der Berechnung des pH-Werts eine Rolle. Die nach dem Schweizer Mathematiker Leonhard Euler benannte eulersche Zahl 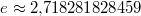 ist (wie 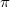 ) eine irrationale Zahl und z. B. definiert als (siehe Fakultät 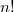 ) 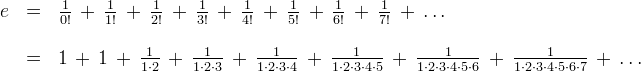 Binomische FormelnBeim Vereinfachen von Summen, die quadriert werden sollen, können für alle reellen Zahlen  und  die Binomischen Formeln helfen. Sie bieten eine Art Abkürzung für das Auflösen von speziellen Klammer termen, die sonst mithilfe des Distributivgesetzes ausmultipliziert werden müssten, z. B. 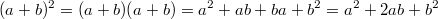 . Das geht natürlich auch - ist aber länger und damit u. U. fehleranfälliger. 1. Binomische Formel: 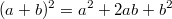 2. Binomische Formel: 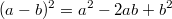 3. Binomische Formel: 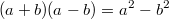 Bemerkung: Bemerkung: Häufig ist es nützlich, die Binomischen Formeln von rechts nach links, d. h. zum Faktorisieren, anzuwenden. TermvereinfachungenBezeichnungskonventionenIn Termen ist es üblich: - Zahlen an den Anfang zu schreiben,
- Variablen (auch in Produkten) alphabetisch zu ordnen und
- sie u. U. so zu erweitern, dass keine Wurzeln im Nenner stehen.
Was darf man mit Termen machen?Man darf: - Zahlen einsetzen und den sich ergebenden Wert ausrechnen
- einen Term in andere einsetzen
- Terme umformen
- Terme vergleichen
Man sagt " ein Term nimmt einen speziellen Wert an", wenn das Einsetzen von irgendeiner Zahl zu diesem speziellen Wert führt, z. B. nimmt der Term 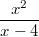 für 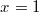 den Wert 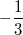 an. Verfahren zur TermvereinfachungZum Vereinfachen von Termen gibt es viele verschiedene Verfahren, da mathematische Terme ebenfalls sehr vielfältig gestaltet sein können. Neben den auf dieser Seite bereits erläuterten Gesetzen kann folgendes helfen: Grundsätzlich kann bei der Behandlung von Termen nicht gesagt werden, welche Form die geschickteste ist. Das hängt stark von der vorgegebenen Aufgabe ab, z. B. erleichtert es das Ableiten, wenn ein Term möglichst wenig Produkte enthält. Umgekehrt ist es zum Kürzen notwendig, dass die Terme faktorisiert vorliegen. Um zu erkennen, welche Umformungen möglich und sinnvoll sind, ist schlicht und einfach viel Übung nötig... |
|
 Brückenkurs
Brückenkurs