Die Berechnung von
Winkel kann im rechtwinkligen Dreieck mithilfe der
inversen
trigonometrischen Funktionen geschehen. Weil
die Winkel hier üblicherweise im Bogenmaß verwendet
werden und das lateinische Worte für "Bogen" "Arkus"
ist, werden diese Funktionen auch
Arkusfunktionen
genannt. Beispielsweise liefert die Arkussinusfunktion
zu einem gegebenen Wert

(der, wie wir unten sehen werden, zwischen
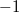
und
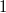
liegen muss) einen Winkel
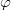
, für den
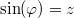
gilt. Die Bezeichnungen, die im Folgenden verwendet
werden, beziehen sich alle wieder auf die Zeichnung am
Anfang der Seite.
Auf dem
Taschenrechner
steht statt
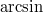
meist
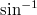
,
statt
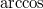
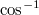
und
statt
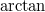
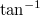
.
Bitte beachten Sie, dass
Auch wenn in diesem Lernmodul vor allem die
Winkelberechnung als Anwendungsfall der
Arkusfunktionen betrachtet wird, sind sie natürlich
für viele andere Bereiche auch nützlich bzw.
notwendig. Wenigstens die Graphen der Arkusfunktionen
sollen nicht fehlen:
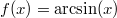
mit dem
Definitionsbereich
![\mathbb{D}=[-1; 1]](./teximg/img1195.png)
und dem
Wertebereich
![\mathbb{W}=\left[-\frac{\pi}{2};\frac{\pi}{2}\right]](./teximg/img1196.png)
als Umkehrfunktion zu
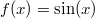
mit
![\mathbb{D}=\left[-\frac{\pi}{2};\frac{\pi}{2}\right]](./teximg/img1198.png)
und
![\mathbb{W}=[-1; 1]](./teximg/img1156.png)
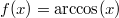
mit
![\mathbb{D}=[-1; 1]](./teximg/img1195.png)
und
![\mathbb{W}=[0;\pi]](./teximg/img1200.png)
als Umkehrfunktion zu
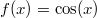
mit
![\mathbb{D}=[0;\pi]](./teximg/img1202.png)
und
![\mathbb{W}=[-1; 1]](./teximg/img1156.png)
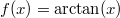
mit
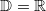
und
![\mathbb{W}=\left[-\frac{\pi}{2};\frac{\pi}{2}\right]](./teximg/img1196.png)
als Umkehrfunktion zu
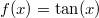
mit
![\mathbb{D}=\left[-\frac{\pi}{2};\frac{\pi}{2}\right]](./teximg/img1198.png)
und
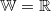
Bemerkung 1:
Bitte beachten Sie, dass der Arkussinus und der
Arkuskosinus nicht für alle reellen Zahlen definiert
sind, sondern nur auf dem
Intervall
![[-1;1]](./teximg/img1205.png)
. Warum
ist das so? Umkehrfunktionen "beantworten"
grundsätzlich die Frage: "Wie lautete das
Argument
der Funktion, wenn wir xy als Ergebnis erhalten
haben?" Die Umkehrfunktion bekommt also das Ergebnis
der Ursprungsfunktion als Argument und liefert das
Argument der Ursprungsfunktion zurück. Nun können
Sinus und Kosinus ja bekanntlich nur Werte zwischen
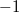
und
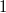
annehmen. Fragen der Art
"Wie lautete das Argument der Sinusfunktion, wenn wir
als Ergebnis
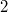
erhalten haben?" sind also sinnlos...
Bemerkung
2: Manchmal müssen beim Bilden von
Umkehrfunktionen die Definitionsbereiche der
ursprünglichen Funktionen eingeschränkt werden, so
auch hier. Warum das? Wegen der Periodizität der
trigonometrischen Funktionen hätte z. B. die Frage
"Wie lautete das Argument der Sinusfunktion, wenn der
Funktionswert
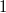
ist?" (also genau die Frage, die
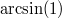
"beantworten" möchte)
nicht nur die Antwort
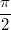
, sondern auch
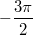
,
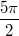
,
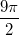
und unendlich viele andere Werte. Ließe man also die
gesamten reellen Zahlen als Definitionsbereich zu,
gäbe es keine eindeutige Antwort. Das ist ein
Widerspruch zur
Funktionsdefinition,
die eine
eindeutige
Zuordnung der Werte verlangt. Man löst das Problem,
indem man die Definitionsbereiche so einschränkt, dass
jeder Funktionswert genau einmal enthalten ist. Das
ist beim Sinus für
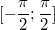
; beim Kosinus für
![[0;\pi]](./teximg/img1212.png)
und beim
Tangens für
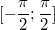
der Fall. Da aus
Bemerkung 1 auch folgt, dass die Wertebereiche der
Umkehrfunktionen den Definitionsbereichen der
ursprünglichen Funktionen entsprechen, kennen wir
somit die Wertebereiche der Arkusfunktionen.
 Brückenkurs
Brückenkurs