Eine Bemerkung vorab: Malpunkte zwischen den Variablen dürfen bei allen Aufgaben auch weggelassen werden. Das ist eigentlich die übliche Schreibweise. In diesem Kapitel wurden sie nur hingeschrieben, um deutlich zu machen, dass hier jeweils multipliziert wird.


1)

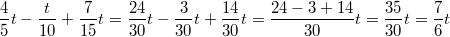Vorgehen: Brüche gleichnamig machen und addieren, anschließend kürzen
Bemerkung 1: Ob die Variable auf oder hinter dem Bruchstrich steht, ist egal.
Bemerkung 2: Da die Variablen alle nur mit Zahlenwerten (und nicht mit weiteren Variablen) multipliziert werden, dürfen diese Koeffizienten einfach addiert bzw. subtrahiert werden.


2)

Vorgehen: Brüche gleichnamig machen und addieren
Bemerkung: Die Variable muss im Hauptnenner berücksichtigt werden, da sie beim dritten Bruch im Nenner steht.


3)

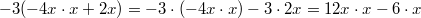Vorgehen: Klammern auflösen
Bemerkung: Auf das Minuszeichen vor der Klammer achten!


4)

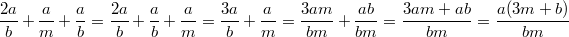Vorgehen: Brüche gleichnamig machen und addieren, anschließend ausklammern
Bemerkung: Den ersten und den dritten Bruch kann man sofort addieren, weil sie bereits den gleichen Nenner haben.


5)

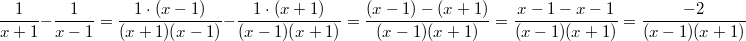Vorgehen: Brüche gleichnamig machen und subtrahieren
Bemerkung 1: Auf das Minuszeichen zwischen den Klammern im Zähler achten! Hier müssen unbedingt Klammern gesetzt werden, da der gesamte Zähler des zweiten Bruches subtrahiert werden muss.
Bemerkung 2: Man könnte im Nenner noch die Klammern auflösen.


6)

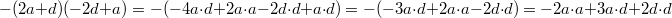Vorgehen: Klammern auflösen
Bemerkung: Auf das Minuszeichen vor den Klammern achten!


7)

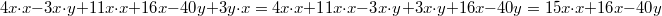Vorgehen: zusammenfassen
Bemerkung 1: Gleiche Produkte von Variablen dürfen addiert und subtrahiert werden. Dabei ändert sich nur der Koeffizient.
Bemerkung 2: Die Reihenfolge der Variablen in einem Produkt ist egal. Üblich ist, die Variablen in alphabetischer Reihenfolge aufzuschreiben, weil das die Übersicht erleichtert.


8)

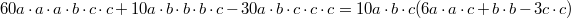Vorgehen: ausklammern


9)

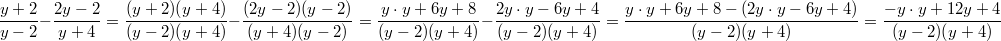Vorgehen: Brüche gleichnamig machen und subtrahieren
Bemerkung 1: Beim Zusammenfassen der Brüche müssen Klammern um den Zähler des zweiten Bruches gesetzt werden, da sich das Minuszeichen sonst nicht auf den gesamten Zähler auswirkt.
Bemerkung 2: Man könnte im Nenner noch die Klammern auflösen.


10)

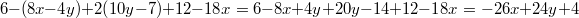Vorgehen: Klammern auflösen, anschließend zusammenfassen

Wichtig: Treffen Punkt- und Strichrechnung aufeinander, müssen Klammern gesetzt werden!

1)


2)


3)


Bemerkung: Um zu berechnen, muss in der entsprechenden Zeile eingesetzt werden. Es ist aber kein Term für gegeben, sondern nur einer für . Daher muss diese Zeile zunächst umgeformt werden.


4)


5)

1) Es handelt sich um eine lineare Gleichung.

2) Es handelt sich nicht um eine lineare Gleichung.

3) Es handelt sich nicht um eine lineare Gleichung.

4) Es handelt sich nicht um eine lineare Gleichung.

5) Es handelt sich um eine lineare Gleichung.

6) Es handelt sich um eine lineare Gleichung.

Ein Hinweis vorweg: Wird eine Gleichung gelöst, sollte das Ergebnis in Form einer Lösungsmenge angegeben werden. Da nach der Rechnung immer geprüft werden muss, ob der berechnete Wert im Definitionsbereich liegt (also ob er als Lösung grundsätzlich infrage kommt), ist die Zahl, die in der letzten Zeile steht, ist nicht automatisch eine Lösung der Gleichung.

Für die Gleichungen 1) bis 5) gilt:

1)


Probe:

Dies ist eine wahre Aussage. Die gefundene Lösung ist also richtig.


2)


Probe:

Dies ist eine wahre Aussage. Die gefundene Lösung ist also richtig.


3)


Bemerkung: Unabhängig davon, welches Element des Definitionsbereichs in diese Gleichung eingesetzt wird, erhält man immer auf beiden Seiten dasselbe Ergebnis. ist schließlich immer richtig... Jede reelle Zahl löst also diese Gleichung, d. h. die Lösungsmenge entspricht dem Definitionsbereich.

4)


Probe:

Dies ist eine wahre Aussage. Die gefundene Lösung ist also richtig.


5)


Bemerkung: Beim Umformen der Gleichung entsteht ein Widerspruch: kann nie stimmen. Daher ist diese Gleichung nicht lösbar. Die Lösungsmenge ist leer.

6)


Bemerkung: Als Definitionsbereich ist hier die Menge der natürlichen Zahlen () gegeben. ist aber bekanntermaßen keine natürliche Zahl (). Also kann für diese Gleichung keine Zahl gefunden werden, die beide Seiten gleich groß werden lässt und im Definitionsbereich liegt. Auch hier ist die Lösungsmenge leer.

Sei die Anzahl der Schüler des Pythagoras'.
Dann "übersetzt" man:

• "die Hälfte studiert Mathematik" mit
• "ein Viertel studiert Physik" mit
• "ein Siebtel lernt das Schweigen" mit

Zusammen ergibt sich also:


Pythagoras hat also Schüler.

Bemerkung zu Textaufgaben allgemein: Der erste Schritt beim Lösen einer Textaufgabe ist immer, sich die benötigten Variablen zu definieren. Anders formuliert: Es muss die Frage "Was ist hier eigentlich gesucht?" beantwortet werden. Das ist zum einen wichtig, um die Logik der Aufgabe zu durchschauen. Zum anderen kann nur dann eine sinnvolle Gleichung formuliert werden, wenn klar ist, was die Variablen genau bezeichnen. Welche Bezeichnung Sie dabei wählen, ist nicht wichtig. Es hat eine gewisse Tradition, die unbekannte Größe zu nennen. Wenn sich aus inhaltlichen Gründen eine andere Bezeichnung anbietet (hier könnte man z. B. die Anzahl der Schüler auch gut nennen), spricht nichts dagegen, diese Bezeichnung zu verwenden. Im Gegenteil, solche Benennungen können helfen, eine möglicherweise komplexere Aufgabe samt Lösung übersichtlich zu halten.
Den Antwortsatz nicht vergessen!