RechenregelnDie folgenden Rechenregeln mögen unspektakulär klingen. Wahrscheinlich sind sie uns ohnehin so in Fleisch und Blut übergegangen, dass man meistens gar nicht merkt, dass man sie anwendet. Dieser Abschnitt soll vor allem bewusst machen, dass es diese Gesetze gibt und dass es nicht selbstverständlich ist, dass sie gelten. So sind beispielsweise die Subtraktion und die Division weder kommutativ noch assoziativ (siehe Beispiele unten). Wenn im Verlauf der Mathematikausbildung weitere mathematische Objekte wie Vektoren und Matrizen hinzukommen, muss immer wieder die Frage gestellt werden, ob genau die Gesetze, die hier so selbstverständlich sind, dafür auch gelten - und nicht überall ist dann auch tatsächlich der Fall. Punktrechnung geht vor Strichrechnung! Das heißt: Eine Kombination aus Summe und Produkt lässt sich nicht ohne Weiteres zusammenfassen. Nur Klammern können diese Reihenfolge ändern. KommutativgesetzDas Kommutativgesetz wird auch Vertauschungsgesetz genannt. Es gilt für alle reellen Zahlen 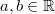 : Im Gegensatz zur Addition und Multiplikation sind die Subtraktion, die Division und die Potenzierung im Bereich der reellen Zahlen nicht kommutativ. Beispiele für kommutative RechenoperationenBeispiele für nicht kommutative Rechenoperationen Subtraktion: | | | | | | | | Division: | | | | | | | | Potenzierung: | | | | | | | |
AssoziativgesetzDas Assoziativgesetz wird auch Verknüpfungs- oder Klammergesetz genannt. Es gilt für alle reellen Zahlen 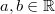 : Daher gilt beispielsweise: 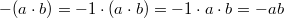 Im Gegensatz zur Addition und Multiplikation sind die Subtraktion, die Division und die Potenzierung im Bereich der reellen Zahlen nicht assoziativ. Beispiele für assoziative RechenoperationenBeispiele für nicht assoziative Rechenoperationen Subtraktion: | | | | | | | | | | | | Division: | | | | | | | | | | | | Potenzierung: | | | | | | | | | | | |
DistributivgesetzDas Distributivgesetz stellt eine Verknüpfung zwischen verschiedenen Rechenoperationen her, z. B. zwischen Multiplikation und Addition bzw. Subtraktion. Es gilt für alle reellen Zahlen 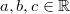 : Linksdistributivität: | | | | Rechtsdistributivität: | | | |
Die Kombination von Division mit Addition bzw. Subtraktion ist nur rechtsdistributiv. Es gilt für alle reellen Zahlen 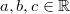 : 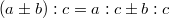 Bemerkung: Das Zeichen 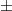 (gesprochen: plusminus) ist eine abkürzende Schreibweise und bedeutet, dass die Gleichung sowohl gilt, wenn an dieser Stelle ein 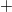 steht als auch, wenn dort ein  steht. Man liest in der Gleichung entweder bei allen Doppelzeichen das Obenstehende oder bei allen Doppelzeichen das Untenstehende. Beispiele für distributive Rechenoperationen Beispiel für nicht distributive Rechenoperationen Das so genannte Ausmultiplizieren (auch "Klammern auflösen" genannt) ist eine direkte Folge des Distributivgesetzes: 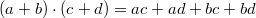 Wendet man diese Rechenvorschrift von rechts nach links an, heißt der Vorgang Ausklammern oder Faktorisieren. Der Begriff "Faktorisieren" deutet darauf hin, dass durch diesen Vorgang ein Produkt entsteht. Eine solche Umformung ist z. B. bei Brüchen und Termen häufig sehr nützlich. Außerdem folgt aus dieser Gesetzmäßigkeit, dass ein Minuszeichen vor einer Klammer alle Vorzeichen in der Klammer ändert. Es gilt nämlich: 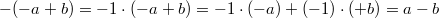 |
|
 Brückenkurs
Brückenkurs