ErklärungenDas ProduktzeichenDas Produktzeichen wird häufig verwendet, um ein Produkt mit mehreren Faktoren zusammengefasst aufzuschreiben. Als Formelzeichen wird der griechische Buchstabe 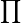 (ein großes Pi) verwendet. In einer Formel: 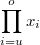 (gesprochen: Produkt von i gleich u bis o über x i) Dabei ist -
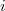 : der Multiplikationsindex oder einfach Index : der Multiplikationsindex oder einfach Index -
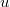 : die untere Multiplikationsgrenze oder einfach untere Grenze, eine ganze Zahl, oft : die untere Multiplikationsgrenze oder einfach untere Grenze, eine ganze Zahl, oft 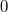 oder oder 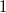 -
 : die obere Multiplikationsgrenze oder einfach obere Grenze, eine ganze Zahl, mindestens so groß wie die untere Multiplikationsgrenze : die obere Multiplikationsgrenze oder einfach obere Grenze, eine ganze Zahl, mindestens so groß wie die untere Multiplikationsgrenze -
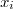 : der Faktor : der Faktor
Beim Auflösen eines Produktzeichens wird genauso vorgegangen, wie beim Summenzeichen beschrieben. Einziger Unterschied: Bei Schritt 14 wird nicht addiert, sondern multipliziert. Der BinomialkoeffizientDer Binomialkoeffizient 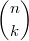 (gesprochen: n über k) wird beim Binomischen Satz und in der Kombinatorik benötigt, nämlich um zu berechnen, wie viele verschiedene k-elementige Teilmengen in einer n-elementigen Menge enthalten sind. Definition: 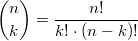 mit 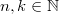 und 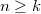 Dabei heißt die Funktion 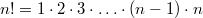 Fakultät Fakultät. Eigenschaften: 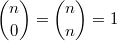 und  und 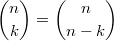 Der Binomische Satz ist Verallgemeinerung der Binomischen Formeln: 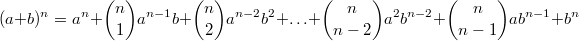 Ein Beispiel Ein Beispiel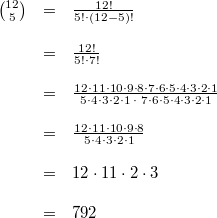 Hinweis: Hinweis: Hier wurde der Übersichtlichkeit wegen in zwei Schritten gekürzt. Im ersten Schritt wurden die Faktoren 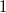 bis 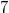 gekürzt. Im zweiten wurden die 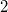 und 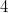 (Nenner) gegen die 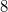 (Zähler), die 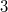 (Nenner) gegen die 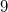 (Zähler) und die 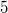 (Nenner) gegen die 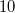 (Zähler) gekürzt. Bemerkung 1: Bei der Berechnung von Binomialkoeffizienten steht sowohl im Zähler als auch im Nenner ein Produkt. Daher kann und sollte vor dem Ausrechnen gekürzt werden. Bemerkung 2: Viele Taschenrechner können Binomialkoeffizienten berechnen. Meist ist die entsprechende Taste mit "nCr" beschriftet. |
|
 Brückenkurs
Brückenkurs