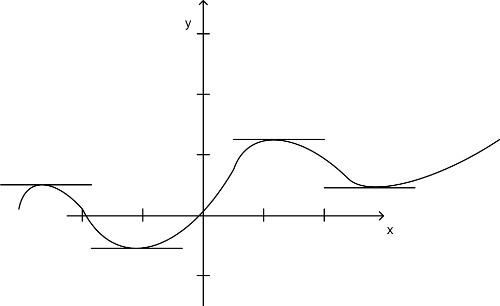
| Abbildung 54: Relative und absolute Maxima und Minima |
gegeben: stetigeableitbare Funktion

Abbildung 54: Relative und absolute Maxima und Minima
Extrema: Waagrechte Tangenten
| relatives Maximum: | y′=0 | y″<0 |
| relatives Minimum: | y′=0 | y″>0 |
.
Hinreichende Bedingung: verschiedenartige Monotoniebögen
Beispiel 13 - 23:
| y=x3 | |
| y′=3x2 | y′(0)=0 |
| y″=6x | y″(0)=0 |
| y‴=6 | y‴(0)=6 |
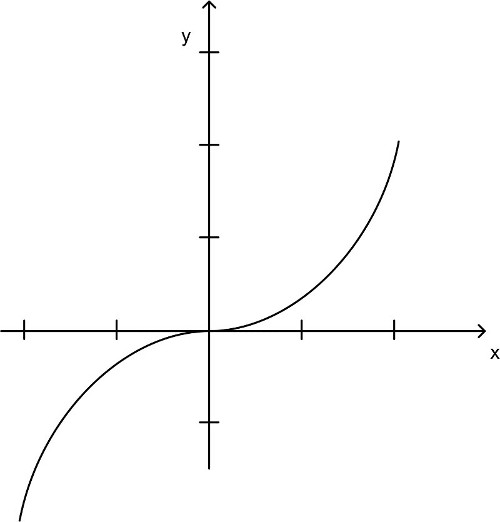
Abbildung 55: Wendepunkt
.
kein Minimum, kein Maximum, sondern Wendepunkt
Beispiel 13 - 24:
y=x4
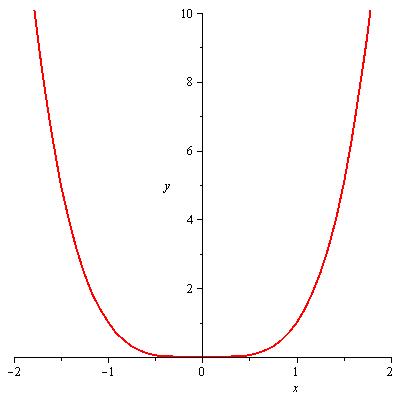
Abbildung 56: Extremum
| y′=4x3 | y′(0)=0 |
| y″=12x2 | y″(0)=0 |
| y‴=24x | y‴(0)=0 |
| y(4)=24 | y(4)(0)=24 |
→ Extrema liegen vor, wenn die 1.Ableitung Null ist und die erste höhere Ableitung, die von Null verschieden ist, von gerader Ordnung ist. f′(x0)=0
| Maxima: | fk(x0)=0 | für 1≤ k ≤ n | und fn(x0) <0 | | n gerade |
| Minima: | fk(x0)=0 | für 1≤ k ≤ n | und fn(x0)>0 | | n gerade |