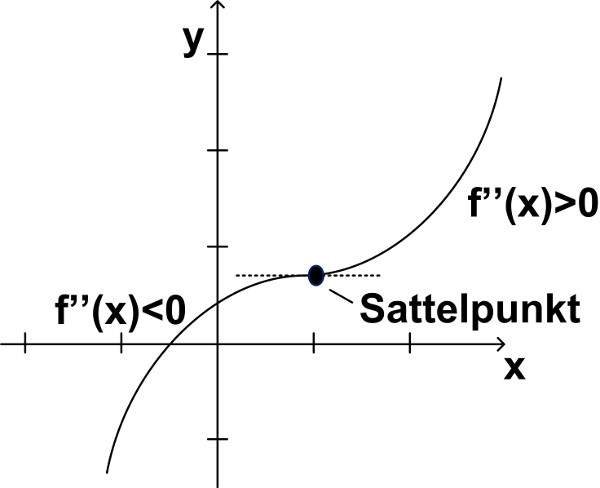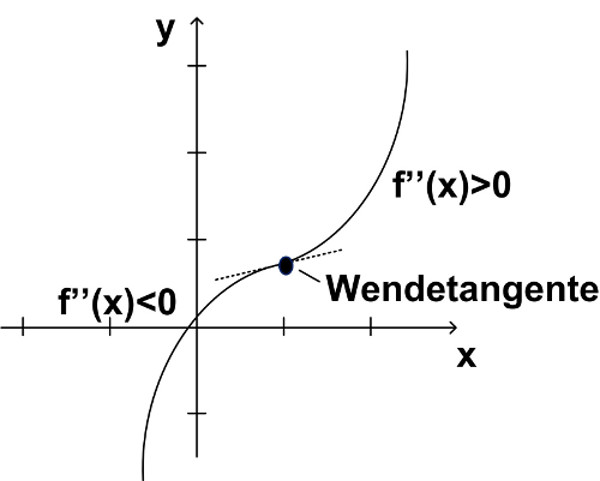
13.3.4  Wendepunkte, Sattelpunkte

---

Abbildung 57: Wendepunkte, Sattelpunkte

---

Ein Wendepunkt liegt vor, wenn f″(x)=0 und die erste höhere von Null verschiedene Ableitung von ungerader Ordnung ist.

.
Beispiel 13 - 25 df9015 .
y=x⁵
.
.
Lösung ansehen .
.

.
Die erste von Null verschiedene Ableitung ist ungerader Ordnung ⇒ Es liegt ein Wendepunkt vor.
.
Beispiel 13 - 26 df9016 .
y=−2/3x³+2x²−2x+2
.
.
Lösung ansehen .
.

.