13.3.9  Diffusion, Arzneimittelverabreichung

Das Modell des pharmakokinetischen Grundversuchs [] ( Kompartiment-Modell ) ist vergleichbar mit dem Modell der Diffusion in der Physik. Es geht aus von Kompartimenten, d.h. pharmakokinetisch einheitlichen Räumen. (In der Sprache der Physik sind dies homogenene Bereiche.) .
Je größer der Konzentrationsunterschied ist, umsomehr versucht C0, kleiner zu werden. (Dies ist eine vereinfachende Modell-Annahme !) .
Beispiel: auf der linken Seite ist eine Konzentration C0, rechts ist C1 = 0 (hierhin ’verdünnt’ sich der Wirkstoff zunächst).

Abbildung 67: Diffusion

.
Dies kann man beschreiben durch .
Konzentrationsänderungsrate =−k · Konzentrationsunterschied (k ist eine Konstante, die -versuchsabhängige- Diffusionskonstante) oder .

dC0
dt
= − ke · C0

oder: .

dC0
C0
= − ke · dt

Eine Lösung der (Differential-)Gleichung (s. Mathematik II)ist:

C0(t)=C0(0)· e−k10t

.
Zu Beginn ist

C0(0)=
D
V

, also die Dosis verteilt auf das Volumen. .

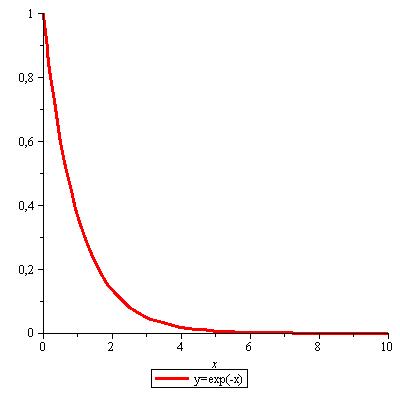
Abbildung 68: Diffusionsverlauf

.

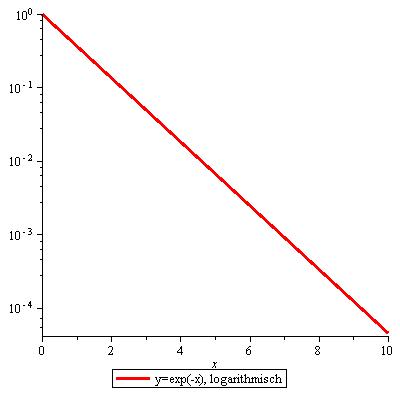
Abbildung 69: Diffusionsverlauf, logarithmische Darstellung

.
Erweiterung: .
Das Zwei-Kompartiment-Modell .
Der Arzneistoff wird in einer ersten Phase injiziert und verteilt sich schnell im gut durchbluteten Gewebe und verteilt sich zwischen den Komparimenten [] . .

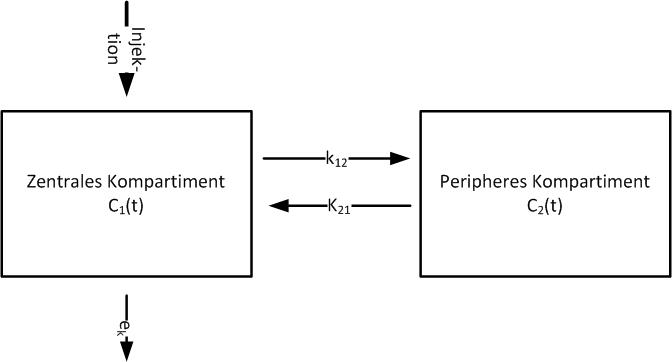
Abbildung 70: Zwei-Kompartiment-Modell

.
Im peripheren Kompartiment kommt es dabei zu einem Anstieg, der nach Erreichung eines Maximums zu einem Abfall und zur Entleerung führt. .
Das Zeitverhalten lässt sich durch zwei gekoppelte Differentialgleichungen beschreiben, die man durch folgende Überlegungen bekommt: .
Die Konzentration C1 im zentralen Kompartiment vermindert sich proportional zur zur momentanen Konzentration durch Elimination mit der Eliminationskonstanten ke: −keC1. .
Des weiteren ändert sich C1 durch den Abfluss in das periphere Kompartiment, was formal ebenfalls einer Elimination entspricht: −k12C1. .
Umgekehrt fließt das Pharmakon aus dem peripheren in das zentrale Kompartiment zurück. Dieser Rückfluss ist proportional zur Konzentration C2 , wird aber positiv gerechnet, da er die Konzentration im zentralen Kompartiment erhöht:

+k21C2

. .
Insgesamt ergibt sich .

dC1
dt
=−(ke+k12)· C1+ k21 C2

.
Im peripheren Kompartiment hat man, bis auf die Elimination, die gleiche Bilanz, nur dass die Vorzeichen umgekehrt gewählt werden müssen, da jeder Verlust des peripheren Kompartiments ein Gewinn des zentralen Kompartiments, und umgekehrt, ist: .

dC2
dt
=k12· C1 − k21 C2

.
Auflösen lässt sich dieses Differentialgleichungssystem (s. Mathematik II), in dem man für C1 und C2 den Ansatz .

C1=A1· e−kα· t + B1· e−kβ· t 

und .

C2=A2· e−kα· t + B2· e−kβ· t 

wählt. .
Zu Beginn ist C1(0)=D/V (also die Dosis verteilt auf das Volumen) und C2(0)=0. .
Mit den Hilfsgrößen .

S=k1+k12+k21

und .

Q=4 · ke· k12

wird .

kα=
1
2
(S+√
S2−Q
)

und .

kβ=
1
2
(S−√
S2−Q
)

. .

Qualitativ sieht die Lösung so aus (für e−0.4t−e−0.5t) .

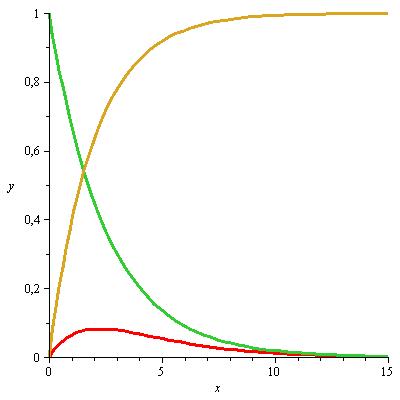
Abbildung 71: Verlauf im Zwei-Kompartiment-Modell

.

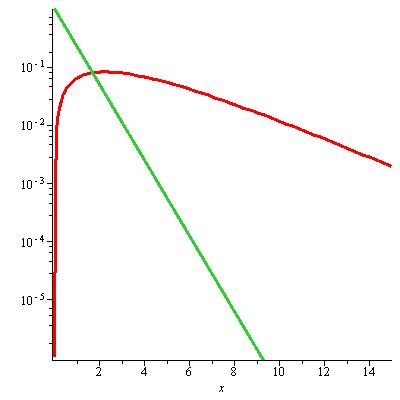
Abbildung 72: Verlauf im Zwei-Kompartiment-Modell, logarithmisch

.