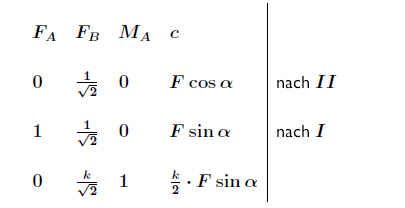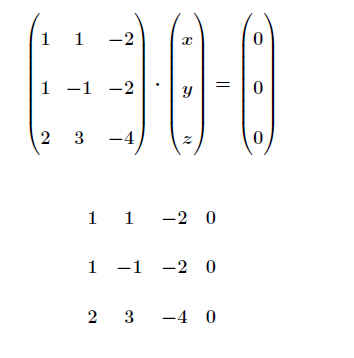Alternativ zum beschriebenen Gauß-Verfahren kann man auch die Koeffizientenmatrix noch weiter umformen, bis man eine Einheitsmatrix E erhält. Damit können die Lösungen direkt abgelesen werden.
A· x→ = c→
A−1 ·A· x→ = A−1 ·c→ oder
x→ = A−1 · c→
Dies ist auch als Gauß-Jordan-Verfahren bekannt.
.
Beispiel 15 - 18
mt9025 .
Alternative Lösung des obigen Beispiels mit Gauß-Jordan: .
.
.
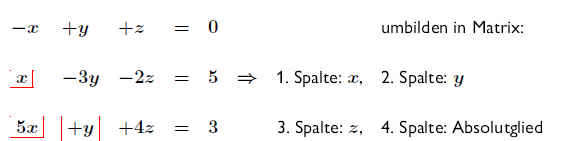(Anm.: Man kann das Absolutglied zuerst auch auf die linke Seite der Gleichung bringen, man muß nur beim Ablesen darauf achten.) .
.
Lösung ansehen .
.
.
Beispiel 15 - 19
mt9010 .
Zu lösen ist das Gleichungssystem .
| −x | +y | −z | = | −2 |
| +y | −2z | = | −4 | |
| −z | = | −15 | ||
.
.
Lösung ansehen .
.
Beispiele zum Gauß’schen Verfahren
.
Beispiel 15 - 20
mt9011 .
Tragwerke
.
.
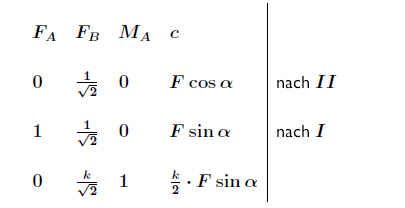Pivotisieren:
.
.
Lösung ansehen .
.
.
Beispiel 15 - 21
mt9012 .
.
.
.
.
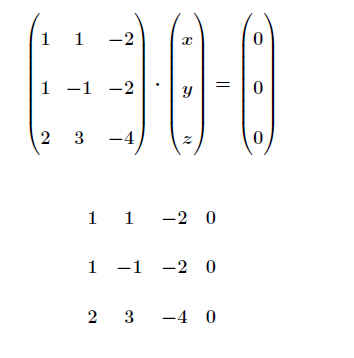Lösung ansehen .
.
.
Beispiel 15 - 22
mt9013 .
| −x1 | +2x2 | +x3 | = | 6 |
| x1 | +x2 | +x3 | = | −2 |
| 2x1 | −4x2 | −2x3 | = | −6 |
.
.
Lösung ansehen .
.
Ein Gleichungssystem hat
.
.
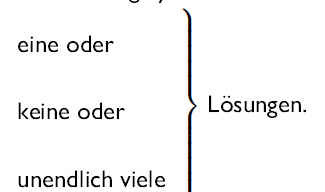Ist das Gleichungssystem ( c→ = 0) homogen, so hat es entweder genau eine Lösung (die Triviallösung x→ = 0→) oder unendlich viele Lösungen (darunter auch die Triviallösung).
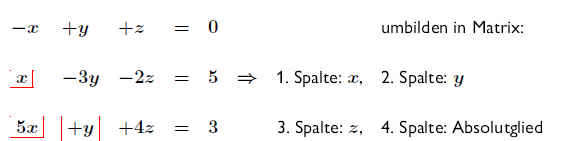