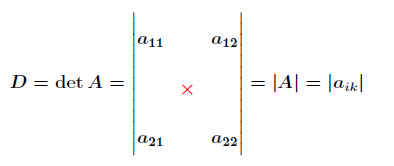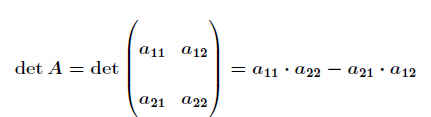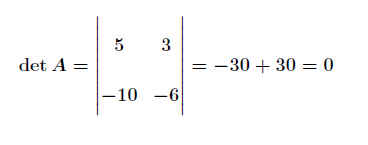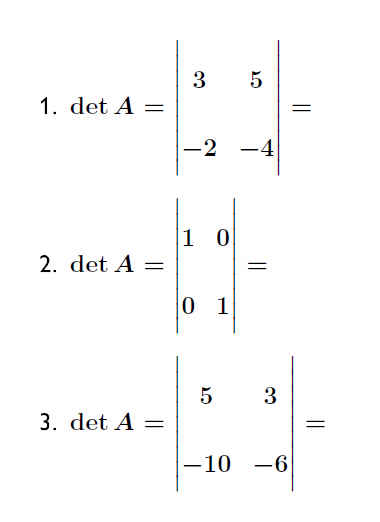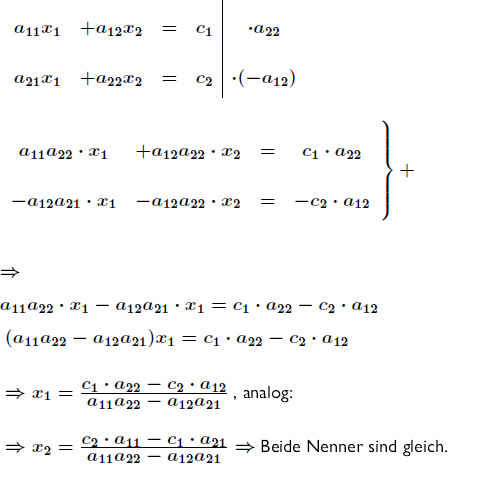16.1.1  zweireihige Determinanten

2× 2 Gleichungssysteme A· x^→=c^→ können wie folgt umgeformt werden:

.
.
Bildet man aus der Koeffizientenmatrix

.
.

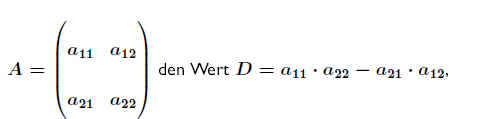hat man die Koeffizientendeterminante der Matrix A bestimmt.
Da die Koeffizientenmatrix eine 2x2-Matrix ist, spricht man von einer 2-reihigen Koeffizientendeterminanten oder Koeffizientendeterminanten 2. Ordnung.
Ist der Wert der Determinanten D=0, so hat das Gleichungssystem keine (bzw. bei einem homogenen Gleichungssystem unendlich viele) Lösung(en).

Determinanten lassen sich nur für quadratische Matrizen (d.h. die Matrix hat genau so viele Zeilen wie Spalten) angeben.

Rechenregel zur Bestimmung einer 2x2-Determinanten: .
.

Die Determinante erhält man, indem man das Produkt der Hauptdiagonal-Elemente bildet und davon das Produkt der Nebendiagonal-Elemente subtrahiert:

.
.

Beispiel 16 - 23:

.
.
.
Beispiel 16 - 24 mt9014 .
.
.
.
Lösung ansehen .
.