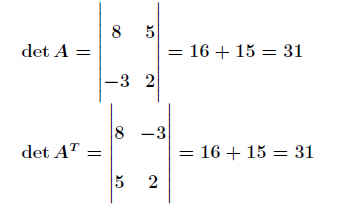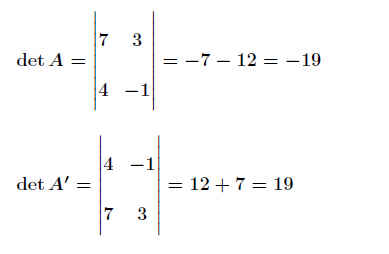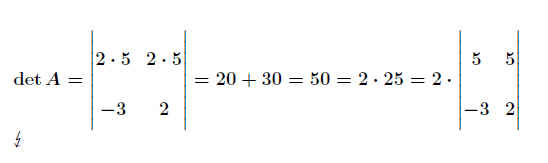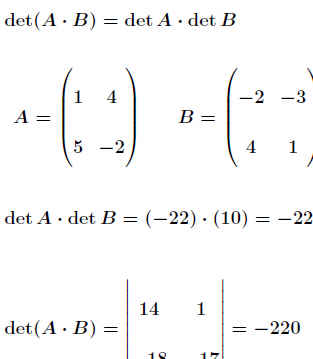16.1.2  allgemeine Rechenregeln für Determinanten

Die hier aufgeführten Rechenregeln gelten auch für Determinanten höherer Ordnung:

1. Der Wert einer Determinante ändert sich nicht, wenn man Zeilen und Spalten vertauscht
2. Beim Vertauschen zweier Zeilen (bzw. Spalten) ändert sich das Vorzeichen
3. Multlipliziert man eine Zeile (bzw Spalte) mit λ, dann multipliziert sich die Determinante
   mit λ
4. Eine Determinante besitzt den Wert 0, wenn
   1. alle Elemente einer Zeile (oder Spalte) Null sind
   2. Zwei Zeilen (oder Spalten) gleich sind
   3. Zwei Zeilen (oder Spalten) zueinander proportional sind
   4. Eine Zeile (oder Spalte) als Linearkombination der übrigen Zeilen (oder Spalten) darstellbar ist.
5. Der Wert einer Determinante ändert sich nicht, wenn man zu einer Zeile (oder Spalte) das Vielfache einer anderen Zeile (oder Spalte) addiert.
6. det(A· B)=detA · detB
7. Dreiecksmatrizen .
   .
   
   
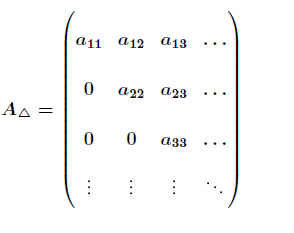   haben als Determinante das Produkt der Hauptdiagonalen
   
   detA_△= a₁₁· a₂₂· a₃₃·…=∏ⁱ a_ii

Beispiel 16 - 25:

1. Der Wert einer Determinante ändert sich nicht, wenn man Zeilen und Spalten vertauscht: .
   .
   .
   
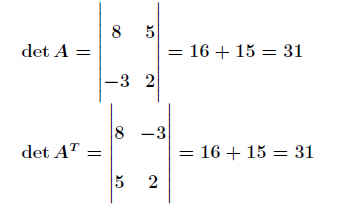2. Beim Vertauschen zweier Zeilen (bzw. Spalten) ändert sich das Vorzeichen: .
   .
   .
   

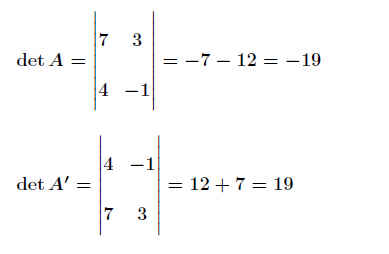3. Multlipliziert man eine Zeile (bzw Spalte) mit λ, dann multipliziert sich die Determinante
   mit λ : .
   .
   .
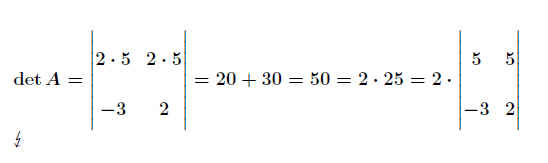   (Achtung! Nicht verwechseln mit der Skalarmultiplikation bei Matrizen!)

4. Eine Determinante besitzt den Wert 0, wenn
   1. alle Elemente einer Zeile (oder Spalte) Null sind
   2. Zwei Zeilen (oder Spalten) gleich sind
   3. Zwei Zeilen (oder Spalten) zueinander proportional sind
   4. Eine Zeile (oder Spalte) als Linearkombination der übrigen Zeilen (oder Spalten) darstellbar ist: .
      

   .
   .
   

5. Der Wert einer Determinante ändert sich nicht, wenn man zu einer Zeile (oder Spalte) das Vielfache einer anderen Zeile (oder Spalte) addiert: .
   .
   .
   
6. .
   .
   
   
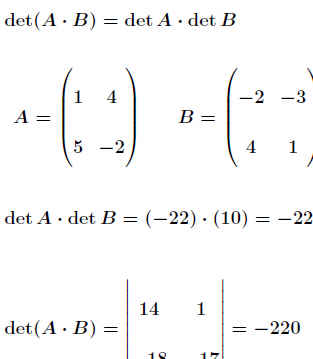7. Dreiecksmatrizen haben als Determinante das Produkt der Hauptdiagonalen
   
   .
   

.
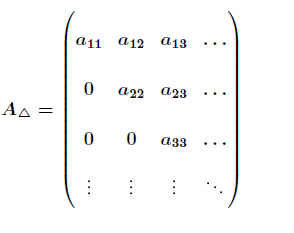