Bildet man aus der Koeffizientenmatrix
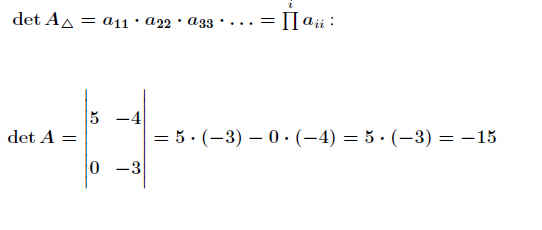 .
. .
den Term
Beispiel 16 - 26:
Gegeben sei ein 3× 3 Gleichungssystem A· x→=c→ ,
ausgeschrieben:
| a11x1 | + a12x2 | + a13x3 | = | c1 |
| a21x1 | + a22x2 | + a23x3 | = | c2 |
| a31x1 | + a32x2 | + a33x3 | = | c3 |
Bildet man aus der Koeffizientenmatrix
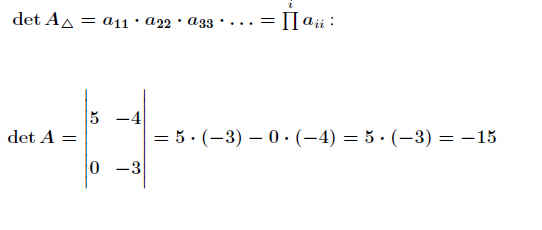 .
.
.
den Term
| D | = | a11 · a22 · a33 | + | a12 · a23 · a31 | + | a13 · a21 · a32 | − |
| − | a13 · a22 · a31 | − | a11 · a23 · a32 | − | a12 · a21 · a33 | , | |
hat man die Koeffizientendeterminante der Matrix A bestimmt.
Ist der Wert der Determinanten D=0, so hat das Gleichungssystem keine (oder unendlich viele) Lösung(en).
Schreibweisen:
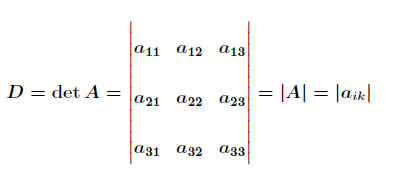 .
.
.
Man spricht hier von dreireihigen Determinanten oder Determinanten 3. Ordnung.
Als Merkregel für die Bestimmung der dreireihigen Determinante von A kann man die Regel von Sarrus verwenden, indem man das Produkt der Hauptdiagonalen addiert und das Produkt der Nebendiagonalen subtrahiert:
(↗ = Nebendiagonale, ↖ = Hauptdiagonale)
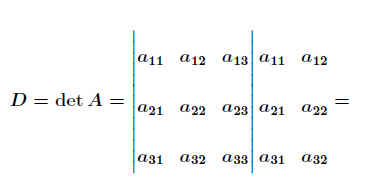 .
.
.
| = | a11 · a22 · a33 | + a12· a23· a31 | + a13 · a21 · a32 − | ||
| − | a13· a22· a31 | − a11 · a23 · a32 | − a12· a21· a33 | ||
.
Beispiel 16 - 27
mt9027 .
Die dreireihige Determinante von A: .
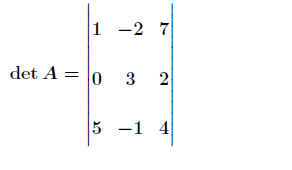 .
.
.
.
.
Lösung ansehen .
.
.
Beispiel 16 - 28
mt9015 .
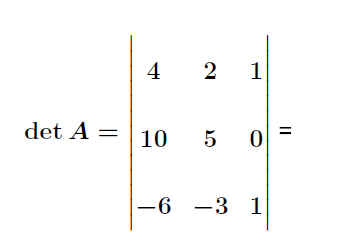 .
.
.
.
.
Lösung ansehen .
.