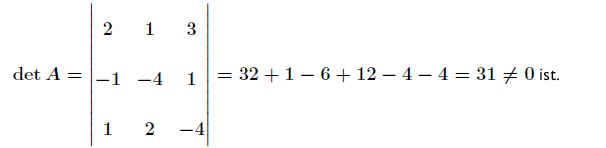16.2.13  Lösung linearer Gleichungssysteme mit der Cramer’schen Regel

Ein lineares (n,n)-Gleichungssystem A · x^→ = c^→ besitzt genau eine Lösung, wenn die Koeffizientenmatrix A regulär ist. Dann existiert auch die zu A inverse Matrix A⁻¹, und die Lösung läßt sich wie folgt berechnen:
Man multipliziert die Matrizengleichung A · x^→ = c^→ von links mit A⁻¹ :
A⁻¹ · A · x^→ = A⁻¹ · c^→

A⁻¹ · c^→ = A⁻¹ · A · x^→ = (A⁻¹ · A)E · x^→ = E · x^→ = x^→

Damit wird der Lösungsvektor
.
.

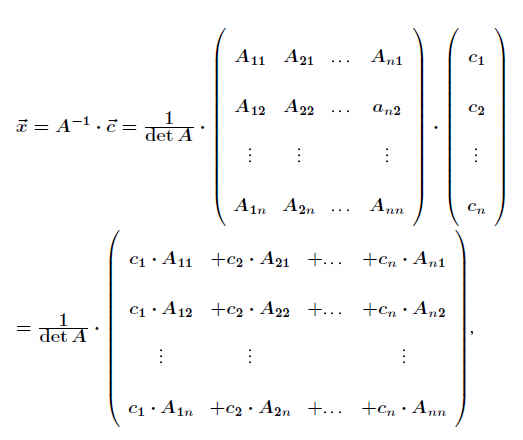oder in komponentenweiser Darstellung:
.
.

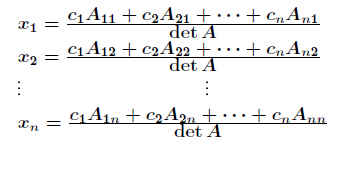Den Zähler kann man auch schreiben als Determinante: .
.

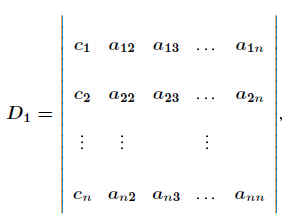was sich sofort verifizieren läßt, indem man einfach diese Determinante nach den Elementen der ersten Spalte entwickelt.
Mit der Vereinbarung D = detA kann man dann vereinfacht schreiben:
x₁ = D₁/D, x₂ = D₂/D, x₃ = D₃/D bzw. x_i = D_i/D,
was als Cramer’sche Regel bekannt ist.

Die Cramer’sche Regel scheint zwar einfach anwendbar, ist aber in der Regel ineffizient, insbesondere bei größeren Zahlen von m und n. .
Beispiel 16 - 42 mt9030
Das Gleichungssystem

.
hat genau eine Lösung, da die Koeffizientendeterminante .
.
.

Anwendung der Cramer’schen Regel: .
.
Lösung ansehen .
.