| Abbildung 87: Wechselverhalten der Getränkekonsumenten |
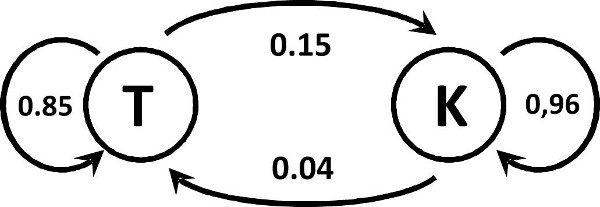
Beispiel 17 - 44: Sie wohnen auf einer recht einsamen Insel. Auf dieser Insel gibt es nur einen Getränkeanbieter mit zwei Getränkesorten T und K. Der Anbieter hat festgestellt, daß pro Jahr 15 % der T-Konsumenten zu K und 4 % von K zu T wechseln. .
Das Konsumentenverhalten kann man graphisch so darstellen: .

Abbildung 87: Wechselverhalten der Getränkekonsumenten
.
Bezeichnet man den Absatz des Getränks K bzw. T in diesem Jahr mit ki und im Folgejahr mit ki+1 bzw. ti und ti+1, kann man die Gleichungen aufstellen: .
| ki+1 | = | 0.85 · ki | + | 0.04 · ti |
| ti+1 | = | 0.15 · ki | + | 0.96 · ti |
.
.
Geht man über zur Matrixschreibweise, ergibt sich der Getränke-(Spalten-)vektor im Folgejahr als Produkt der Übergangsmatrix M mit dem Getränke-(Spalten-)vektor des Vorjahres: .
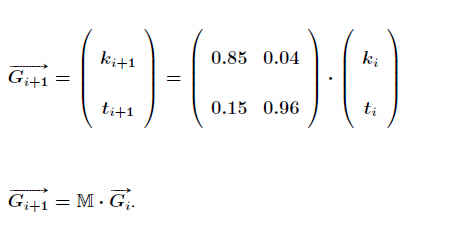 .
.
.
.
Gi+1→ = M · Gi→ . .
Für einen Anfangs-Absatz von .
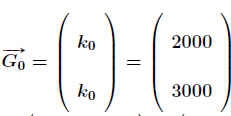 .
.
.
.
Fässern erhält man im Folgejahr einen Verkauf von .
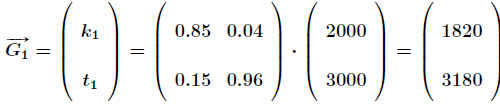 .
.
.
.
Fässern. .
.
Im Folgejahr (gleiches Wechselverhalten vorausgesetzt) ergibt sich .
.
ein Verkauf von .
.
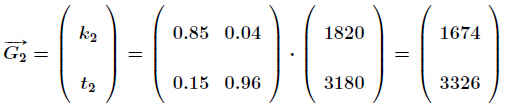 .
.
.
.
Fässern. .
.
Interpretiert man den jährlichen Verkauf von Getränkefässern als Beobachtung und die Wechselraten als (feste) ’Wahrscheinlichkeiten’, so können wir bei bekannten Verkaufszahlen eines Jahres auf die Verkaufszahlen im Folgejahr schließen. .
Derartige Prognosemodelle, die mit der Verkettung von Wahrscheinlichkeiten operieren, nennt man Markoff’sche Ketten : Jede Beobachtung ist nur von einer oder von einer beschränkten Anzahl vorhergehender Beobachtungen abhängig. .