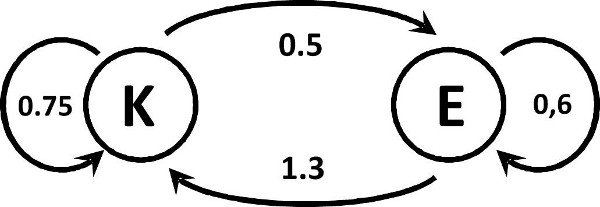
| Abbildung 88: Leslie-Diagramm |
In Analogie zu obigem Getränkebeispiel soll die Populationsentwicklung einer Schwalbenherde betrachtet werden. Bekannt seien die (jährliche) Existenzwahrscheinlichkeit von Küken (K) L11 = 0.75 (im Folgejahr sind nur noch drei Viertel übrig) sowie Erwachsener (E) von L22 = 0.6. Jährlich wird die Hälfte der Küken erwachsen (L21 = 0.5), und jährlich gebären die erwachsenen Schwalben 1.3-fachen Nachwuchs (L12 = 1.3). .
Im Leslie-Diagramm werden die Übergangswahrscheinlichkeiten an den Pfeilen eingetragen. Ist eine Übergangswahrscheinlichkeit Null, so kann der Pfeil weggelassen werden. .

Abbildung 88: Leslie-Diagramm
Nun seien in einem Bestand 30 Erwachsene und 60 Küken. Wie groß ist der Bestand nach einem bzw. 2 Jahren ? .
Derartige Übergangsmatrizen (sie sind analog zu oben) werden in der theoretischen Ökologie zur Beschreibung von Populationen genutzt und wurden von P. H. Leslie formuliert. Hat man Daten über n Altersklassen, dann ist die
Leslie-Matrix vomn Typ nxn. .
In unserem Beispiel lautet sie: .
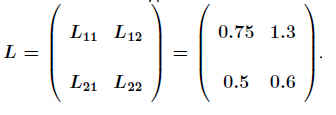 .
.
.
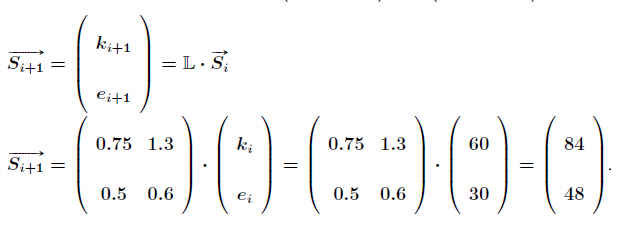 .
.
.
Für das Folgejahr ist die Population: .
.
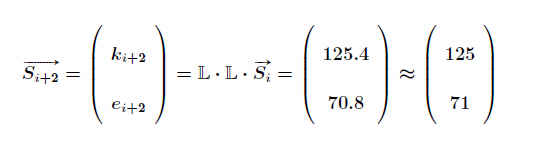 .
.
.