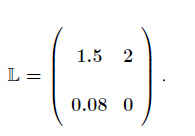17.1.3  Eigenwerte und Eigenvektoren

Gegeben sei folgende Leslie-Matrix: .
.
.
.
Für einen Populationsvektor .
.
.
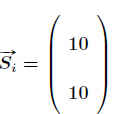ergibt sich im Folgejahr .
.
.
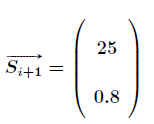Für einen anderen Populationsvektor .
.
.
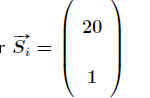ergibt sich im Folgejahr .
.
.
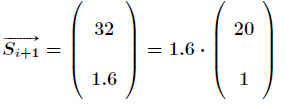Das heißt, der Populationsvektor kann aus dem ursprünglichen Vektor durch Multiplikation .
mit 1.6 erzeugt werden. Wenn das Produkt einer Matrix L mit einem Vektor s^→ das Gleiche ergibt wie die Multiplikation des Vektors s^→ mit einer Zahl λ, nennen wir diesen Vektor Eigenvektor . Die Zahl λ bezeichnet man als Eigenwert . .
Wie findet man die Eigenwerte und Eigenvektoren ? .
Wir gehen von folgendem Ansatz aus: L· s^→ = λ · s^→ .
Ergänzt um die Einheitsmatrix I .
L· s^→ = λ · I· s^→ .
L· s^→ − λ · I· s^→ =0 .
(L − λ · I)· s^→ =0 .
Diese Gleichung ist für von Null verschiedene Vektoren s^→ dann erfüllt, wenn .
.
.
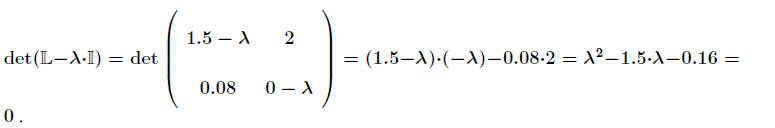Lösungen sind λ₁ = 1.6 und λ₂ = − 0.1. .
Die Eigenvektoren erhält man nun, indem man das Gleichungssystem .
L· s^→ = λ · s^→ jeweils für die Werte von λ₁ und λ₂ löst. .
Für λ₁ =1.6 ergibt sich: .
.
.

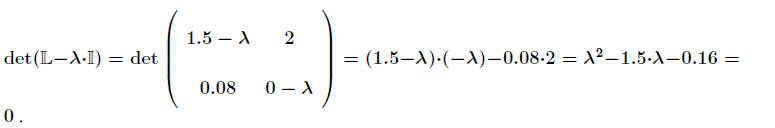Für λ₂ =−0.1 erhält man unendlich viele Lösungen: 0.8 · s₁ = s₂ .
Sind nun die Populationsgrößen Eigenvektoren der Leslie-Matrizen, so kann man die Folgepopulationen einfach durch (ggf. mehrfache) Multiplikation des Eigenwerts mit dem Vektor bestimmen: .
s_i+n^→ = λⁿ · s_i^→ . .