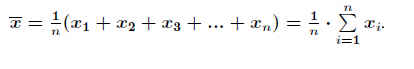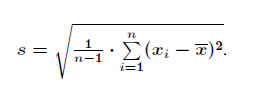18.5.7  Gaußsche Normalverteilung

In einer Vielzahl von technischen Vorgängen kann bei einer stetigen Verteilung mit großer Genauigkeit eine Gaußsche Normalverteilung angenommen werden. Die Dichtefunktion ist eine Funktion der Klasse .
f(x) ∝ exp^−x2/2. .
.
Die Lage der Verteilungsfunktion wird oft durch eine Verschiebung des x-Werts um µ angegeben, die ’Breite’ der Kurve durch einen Faktor σ. .
Man kann einen Vorfaktor bestimmen, um die Gesamtfläche unter der Dichtefunktion auf den Wert 1 zu bringen. Damit erhält man die normierte Dichtefunktion .
.
.
.
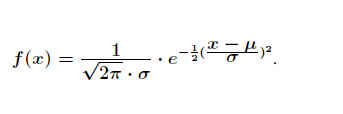µ : Mittelwert .
σ : Standardabweichung. .

---

Abbildung 96: Normalverteilung mit σ= 1; 0,75; 0,5

---

Im Bereich µ − σ und µ + σ liegen 68,3 % der Werte. .
Im Bereich µ − 2σ und µ + 2σ liegen 95,5 % der Werte. .
Im Bereich µ − 3σ und µ + 3σ liegen 99,7 % der Werte. .
.
Für eine normalverteilte Meßreihe gilt: .
Als ’bester’ Schätzwert für den unbekannten ’wahren’ Wert µ der Meßgröße ’X’ gilt der .
arithmetische Mittelwert .
.
.
.
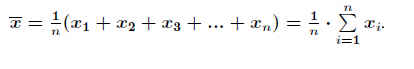Ein geeignetes Maß für die Streuung der Einzelmessungen x_i ist die Standardabweichung .
.
.
.
.
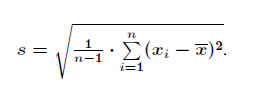Für jeden Mittelwert kann man eine Standardabweichung s _x des Mittelwerts x angeben: .
.
.
.
Sie beschreibt die Streuung der Mittelwerte (die man aus mehreren Messreihen erhalten hat) um den ’wahren’ Mittelwert µ. .
.

Beispiel 18 - 16 st9050
Eine Tabelle mit Werten der Verteilungsdichte f(z) = 1/√2π· exp(−z²/2) kann angelegt werden mittels der Funktion .
NORM.S.VERT(z, WAHR) .
.
Der Wert für z muß ggf. normiert werden: z= x−µ/ σ .
.

Lösung ansehen .
.

.

Die Dichtefunktion

• ist spiegelsymmetrisch zur Geraden x = µ
• Das Maximum liegt bei µ
• Die beiden Wendepunkte liegen symmetrisch zu µ an den Stellen x_2,3=µ ± σ
• Die Fläche unter der Dichtefunktion hat den Wert 1
• ca. 67 % der Ereignisse liegen zwischen x ± µ/σ, ca. 97% liegen in der sogenannten 2-σ-Grenze.

Die Excel-Funktion NORM.S.VERT(x;FALSCH) gibt die Werte der Verteilungsdichte, die Excel-Funktion NORM.S.VERT(x;WAHR) gibt die Werte der Verteilungsfunktion einer standardnormalverteilten Zufallsvariablen x zurück. .
(Frage: Wieviel Prozent liegen außerhalb der 6-σ-Grenze ? -> 99,9999998 % ) .
Die Funktion NORM.S.INV(Wert) gibt Quantile der Standardnormalverteilung zurück (Umkehrfunktion). .

Beispiel 18 - 17 st9052
In einem Werk werden Kunststoffteile hergestellt, deren Durchmesser einer Normalverteilung folgen mit dem Mittelwert µ = 20 mm und der Standardabweichung σ = 0,4 mm. Der Kunde toleriert nur Teile, die höchstens 20,6 mm dick sind. Welcher Anteil an Ausschuss ist zu erwarten ?

.
Lösung ansehen .
.

.
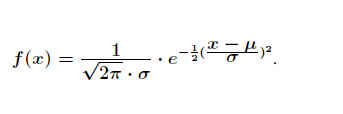