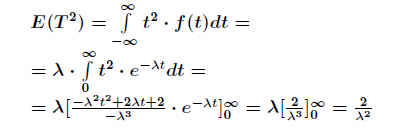Folgt eine stetige Zufallsvariable der Dichtefunktion .
.
.
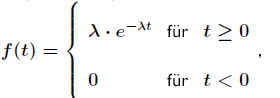so nennt man sie exponentialverteilt. .
Diese Dichtefunktion kennen wir vom radioaktiven Zerfall: Die Wachrscheinlichkeit, daß ein Teil zerfällt, ist konstant. .
Häufig wird so die Lebensdauer T eines bestimmten elektronischen Bauelements beschrieben. .
Für die Verteilungsfunktion gilt: .
.
.
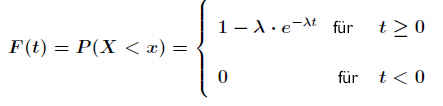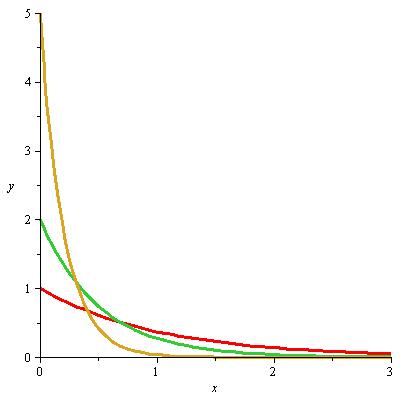
Abbildung 97: Exponential-Verteilungsdichte für λ = 1; 2 ; 5
.
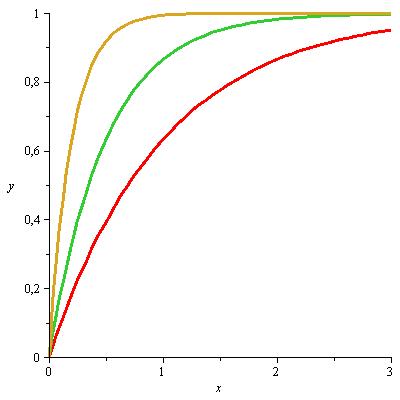
Abbildung 98: Exponential-Verteilungsfunktion für λ = 1; 2 ; 5
.
Der Erwartungswert (mittlere Lebensdauer) kann so ermittelt werden zu (s. Formelsammlung): .
E(T) = ∫−∞∞ t · f(t) dt = λ · ∫0∞ t · e− λ t dt =
= 1/λ [ ( −λ t − 1)· e−λ t ]0∞ = 1/λ .
.
Für die Varianz erhält man: .
.
.
.
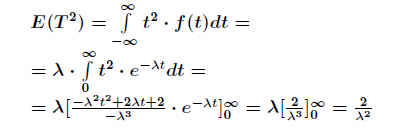Damit beträgt σ2 = E(T2) − µ2 = 2/λ2 − 1/λ2 = 1/λ2 .
.
Die Standardabweichung beträgt folglich σ = 1/λ .
Beispiel 18 - 18 st9070
Die mittlere Lebensdauer einer Energiesparleuchte ist mit 10.000 Stunden angegeben. Wie groß ist die Wahrscheinlichkeit, daß eine Energiesparleuchte aus dieser Charge auch nach 15.000 noch Stunden brennt ?
.
Lösung ansehen .
.
.
(Anm.: Will man zeitabhängige Erscheinungen berücksichtigen, wird häufig die Weibull-Verteilung eingesetzt (s. []) mit der Dichte-Verteilung .
f(t)=λ · k · (λ · t)k−1e(λ · t)k).
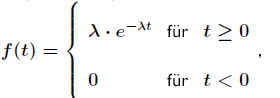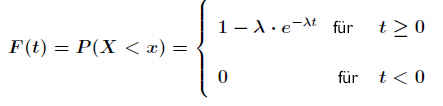