Gosset zeigte, daß der Quotient aus .
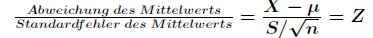 .
. .
.
nur dann einer Standardnormalverteilung folgt, wenn die die Xi normalverteilt sind und µ und σ bekannt sind. .
Die als Student-verteilung oder auch als t-Verteilung bekannte Verteilung wurde von W.S. Gosset unter dem Pseudonym ’Student’ erarbeitet [], []. .
Gosset zeigte, daß der Quotient aus .
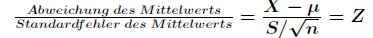 .
.
.
.
nur dann einer Standardnormalverteilung folgt, wenn die die Xi normalverteilt sind und µ und σ bekannt sind. .
Wenn die unabhängigen Zufallsvariablen X1, X2,...,Xn identisch normalverteilt sind, dann unterliegt die stetige Zufallsgröße t einer Studentschen (t-) Verteilung: .
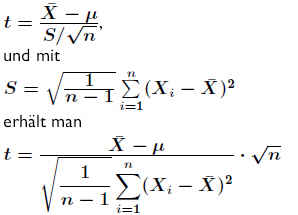 .
.
.
.
Der Freiheitsgrad FG = (n−a) =ν ist definiert als die Anzahl frei verfügbarer Beobachungen, also dem Stichprobenumfang minus der Anzahl a der Parameter, die aus der Stichprobe geschätzt werden. .
Für eine steigende Anzahl an Freiheitsgraden ν nähert sich die Student-t-Verteilung der Normalverteilung immer näher an. Als Faustregel gilt, dass man ab ca. ν > 30 die Student-t-Verteilung bei Bedarf durch die Normalverteilung approximieren kann. .
Die Student-t-Verteilung wird zur Konfidenzschätzung für den Erwartungswert einer normalverteilten Zufallsvariable bei unbekannter Varianz verwendet. .
Die Wahrscheinlichkeitsdichte ist gegeben durch .
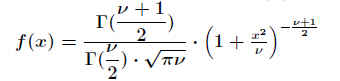 .
.
.
.
( Γ() ist die Gamma-Funktion, Γ(x)= ∫0∞tx−1e−t für x>0). .
Bestimmung der Werte über Aufruf in Excel:
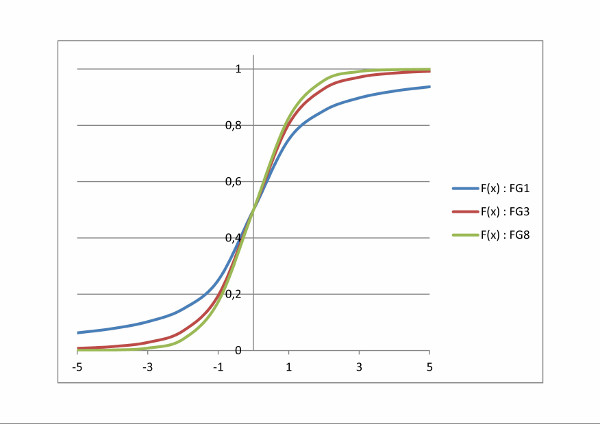
Abbildung 99: Wahrscheinlichkeitsdichte und -funktion der t-Verteilung für ν = 1,3,8
Tabelle einiger t-Quantile für verschiedene (zweiseiteige) Vertrauensniveaus γ (aus []);
(Linke Spalte: ν - Anzahl der Freiheitsgrade) .
| ν | γ = 0,5 | 0,75 | 0,8 | 0,9 | 0,95 | 0,98 | 0,99 | 0,998 |
| 1 | 1,000 | 2,414 | 3,078 | 6,314 | 12,706 | 31,821 | 63,657 | 318,309 |
| 2 | 0,816 | 1,604 | 1,886 | 2,920 | 4,303 | 6,965 | 9,925 | 22,327 |
| 3 | 0,765 | 1,423 | 1,638 | 2,353 | 3,182 | 4,541 | 5,841 | 10,215 |
| 4 | 0,741 | 1,344 | 1,533 | 2,132 | 2,776 | 3,747 | 4,604 | 7,173 |
| 5 | 0,727 | 1,301 | 1,476 | 2,015 | 2,571 | 3,365 | 4,032 | 5,893 |
| 6 | 0,718 | 1,273 | 1,440 | 1,943 | 2,447 | 3,143 | 3,707 | 5,208 |
| 7 | 0,711 | 1,254 | 1,415 | 1,895 | 2,365 | 2,998 | 3,499 | 4,785 |
| 8 | 0,706 | 1,240 | 1,397 | 1,860 | 2,306 | 2,896 | 3,355 | 4,501 |
| 9 | 0,703 | 1,230 | 1,383 | 1,833 | 2,262 | 2,821 | 3,250 | 4,297 |
| 10 | 0,700 | 1,221 | 1,372 | 1,812 | 2,228 | 2,764 | 3,169 | 4,144 |
| 11 | 0,697 | 1,214 | 1,363 | 1,796 | 2,201 | 2,718 | 3,106 | 4,025 |
| 12 | 0,695 | 1,209 | 1,356 | 1,782 | 2,179 | 2,681 | 3,055 | 3,930 |
| 13 | 0,694 | 1,204 | 1,350 | 1,771 | 2,160 | 2,650 | 3,012 | 3,852 |
| 14 | 0,692 | 1,200 | 1,345 | 1,761 | 2,145 | 2,624 | 2,977 | 3,787 |
| 15 | 0,691 | 1,197 | 1,341 | 1,753 | 2,131 | 2,602 | 2,947 | 3,733 |
| 16 | 0,690 | 1,194 | 1,337 | 1,746 | 2,120 | 2,583 | 2,921 | 3,686 |
| 17 | 0,689 | 1,191 | 1,333 | 1,740 | 2,110 | 2,567 | 2,898 | 3,646 |
| 18 | 0,688 | 1,189 | 1,330 | 1,734 | 2,101 | 2,552 | 2,878 | 3,610 |
| 19 | 0,688 | 1,187 | 1,328 | 1,729 | 2,093 | 2,539 | 2,861 | 3,579 |
.
| ν | γ = 0,5 | 0,75 | 0,8 | 0,9 | 0,95 | 0,98 | 0,99 | 0,998 |
| 20 | 0,687 | 1,185 | 1,325 | 1,725 | 2,086 | 2,528 | 2,845 | 3,552 |
| 21 | 0,686 | 1,183 | 1,323 | 1,721 | 2,080 | 2,518 | 2,831 | 3,527 |
| 22 | 0,686 | 1,182 | 1,321 | 1,717 | 2,074 | 2,508 | 2,819 | 3,505 |
| 23 | 0,685 | 1,180 | 1,319 | 1,714 | 2,069 | 2,500 | 2,807 | 3,485 |
| 24 | 0,685 | 1,179 | 1,318 | 1,711 | 2,064 | 2,492 | 2,797 | 3,467 |
| 25 | 0,684 | 1,178 | 1,316 | 1,708 | 2,060 | 2,485 | 2,787 | 3,450 |
| 30 | 0,683 | 1,173 | 1,310 | 1,697 | 2,042 | 2,457 | 2,750 | 3,385 |
| 40 | 0,681 | 1,167 | 1,303 | 1,684 | 2,021 | 2,423 | 2,704 | 3,307 |
| 50 | 0,679 | 1,164 | 1,299 | 1,676 | 2,009 | 2,403 | 2,678 | 3,261 |
| 100 | 0,677 | 1,157 | 1,290 | 1,660 | 1,984 | 2,364 | 2,626 | 3,174 |
| 200 | 0,676 | 1,154 | 1,286 | 1,653 | 1,972 | 2,345 | 2,601 | 3,131 |
| 500 | 0,675 | 1,152 | 1,283 | 1,648 | 1,965 | 2,334 | 2,586 | 3,107 |
| ∞ | 0,674 | 1,150 | 1,282 | 1,645 | 1,960 | 2,326 | 2,576 | 3,090 |
.
Man kann beispielsweise ein Intervall angeben, das den unbekannten Mittelwert µ mit einer vorgegebenen Wahrscheinlichkeit P=γ überdeckt. Dies entspricht dem Vertrauensintervall mit den Grenzen .
.
x− t · s/ √n ≤ µ ≤ x + t · s/ √n .
.
Die halbe Breite des Vertrauensbereiches wird als Meßunsicherheit Δ x bezeichnet: .
.
Δ x = t · s/ √n, .
.
womit man auch schreiben kann: .
.
x− Δ x ≤ µ ≤ x+ Δ x .
.
bzw. .
.
|x− Δ x| ≤ µ . .
.
Der Wert von t hängt von der Anzahl n der Meßwerte und dem Vertrauensniveau ab, das man vorgibt. Häufig wird γ = 95 % und 99% verwendet. .
Für eine sehr große Zahl von Messwerten oder bei bekannter Stabdardabweichung σ (der normalverteilten Grundgesamtheit) geht diese Verteilung in die Gaußsche Verteilung über. .
.
Meist gibt man für einen Messwert x und dessen Vertrauensbereich das Ergebnis in der Form an: .
x = x ± Δ x = x ± t · s/ √n .
.