Die Wahrscheinlichkeitsdichte kann angegeben werden zu .
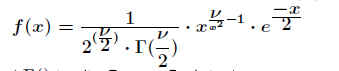 .
. .
.
( Γ() ist die Gamma-Funktion). .
Die Summe Zi= X12+ X22+...Xn2 von n unabhängigen quadrierten standardnormalverteilten Zufallsvariablen genügt einer Chi-Quadrat-Verteilung mit n Freiheitsgraden. .
Die Wahrscheinlichkeitsdichte kann angegeben werden zu .
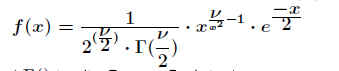 .
.
.
.
( Γ() ist die Gamma-Funktion). .
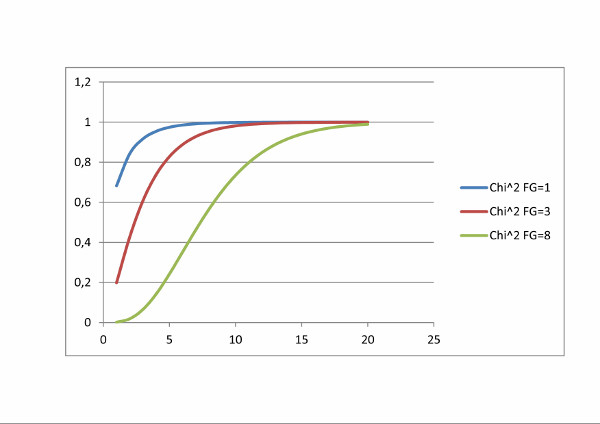
Abbildung 100: Wahrscheinlichkeitsdichte und -funktion der Chi-Quadrat-Verteilung für ν = 1;3 und 8
Quantile der Chi-Quadrat-Verteilung für verschiedene Vertrauensniveaus (aus []);
(Linke Spalte: ν - Anzahl der Freiheitsgrade) .
| ν | 0,005 | 0,01 | 0,025 | 0,05 | 0,1 | 0,5 | 0,9 | 0,95 | 0,975 | 0,99 | 0,995 |
| 1 | 0,00 | 0,00 | 0,00 | 0,00 | 0,02 | 0,45 | 2,71 | 3,84 | 5,02 | 6,63 | 7,88 |
| 2 | 0,01 | 0,02 | 0,05 | 0,10 | 0,21 | 1,39 | 4,61 | 5,99 | 7,38 | 9,21 | 10,60 |
| 3 | 0,07 | 0,11 | 0,22 | 0,35 | 0,58 | 2,37 | 6,25 | 7,81 | 9,35 | 11,34 | 12,84 |
| 4 | 0,21 | 0,30 | 0,48 | 0,71 | 1,06 | 3,36 | 7,78 | 9,49 | 11,14 | 13,28 | 14,86 |
| 5 | 0,41 | 0,55 | 0,83 | 1,15 | 1,61 | 4,35 | 9,24 | 11,07 | 12,83 | 15,09 | 16,75 |
| 6 | 0,68 | 0,87 | 1,24 | 1,64 | 2,20 | 5,35 | 10,64 | 12,59 | 14,45 | 16,81 | 18,55 |
| 7 | 0,99 | 1,24 | 1,69 | 2,17 | 2,83 | 6,35 | 12,02 | 14,07 | 16,01 | 18,48 | 20,28 |
| 8 | 1,34 | 1,65 | 2,18 | 2,73 | 3,49 | 7,34 | 13,36 | 15,51 | 17,53 | 20,09 | 21,95 |
| 9 | 1,73 | 2,09 | 2,70 | 3,33 | 4,17 | 8,34 | 14,68 | 16,92 | 19,02 | 21,67 | 23,59 |
| 10 | 2,16 | 2,56 | 3,25 | 3,94 | 4,87 | 9,34 | 15,99 | 18,31 | 20,48 | 23,21 | 25,19 |
| 15 | 4,60 | 5,23 | 6,26 | 7,26 | 8,55 | 14,34 | 22,31 | 25,00 | 27,49 | 30,58 | 32,80 |
| 20 | 7,43 | 8,26 | 9,59 | 10,85 | 12,44 | 19,34 | 28,41 | 31,41 | 34,17 | 37,57 | 40,00 |
| 25 | 10,52 | 11,52 | 13,12 | 14,61 | 16,47 | 24,34 | 34,38 | 37,65 | 40,65 | 44,31 | 46,93 |
| 30 | 13,79 | 14,95 | 16,79 | 18,49 | 20,60 | 29,34 | 40,26 | 43,77 | 46,98 | 50,89 | 53,67 |
| 35 | 17,19 | 18,51 | 20,57 | 22,47 | 24,80 | 34,34 | 46,06 | 49,80 | 53,20 | 57,34 | 60,28 |
| 40 | 20,71 | 22,16 | 24,43 | 26,51 | 29,05 | 39,34 | 51,80 | 55,76 | 59,34 | 63,69 | 66,77 |
.