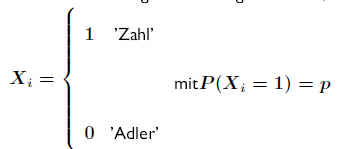 .
. .
.
Damit kann man folgende Aussagen über die Münze treffen: .
p=1/2 ⇔ Münze fair .
p>1/2 ⇔ Zahl häufiger .
Nullhypothese: H0: p=1/2 .
Alternativhypothese: H1: p>1/2 .
.
Der Binomialtest wird verwendet, um Hypothesen über Merkmale zu prüfen, die genau zwei Ausprägungen annehmen können (dichotome Merkmale).
Der Test wird anhand des Modells der Binomialverteilung durchgeführt. .
Hierzu zerlegen wir den Stichprobenraum M in zwei Teilmengen K0 und K1. Die Nullhypothese wird
K0 heißt Annahmebereich , K1 heißt kritischer Bereich .
.
Beispiel 19 - 19
st9080 .
Es wird behauptet, daß beim Werfen von 2 Euro -Münzen öfters die Zahl erscheint als der Adler. .
Es wird nun 10 mal geworfen. .
Ab wann sind Zweifel an der Fairness gerechtfertigt ? Wenn
Keines dieser Ereignisse ist ausgeschlossen, auch wenn die Münze fair ist. .
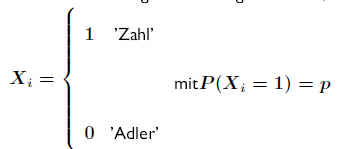 .
.
.
.
Damit kann man folgende Aussagen über die Münze treffen: .
p=1/2 ⇔ Münze fair .
p>1/2 ⇔ Zahl häufiger .
Nullhypothese: H0: p=1/2 .
Alternativhypothese: H1: p>1/2 .
Prüfgröße Y=∑i=110Xi .
Wenn also Y>c, wird die Nullhypothese verworfen. .
c muss geeignet gewählt werden. .
Wir können annehmen, daß die einzelnen Würfe unabhängig voneinander sind. .
Damit ist zu prüfen, ob die Prüfgröße binomial verteilt ist: .
Y=∑i=110Xi für H0: Y ∼
Binomial(n=10, p=0,5) .
.
Binomialverteilung :
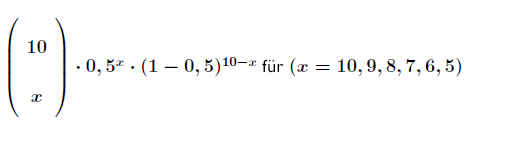 .
.
.
.
.
Formel: =BINOM.VERT(x;10;0,5;FALSCH) .
| x | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| P(x) | 0,001 | 0,010 | 0,044 | 0,117 | 0,205 | 0,246 | 0,205 | 0,117 | 0,044 | 0,010 | 0,001 |
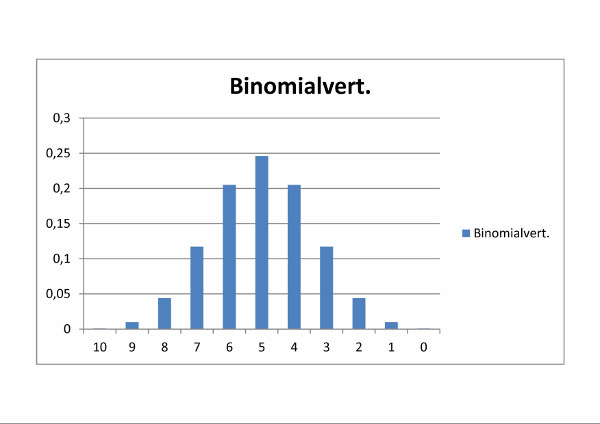
Abbildung 101: Binomialverteilung des Wurfexperiments
.
Die Nullhypothese kann als erfüllt betrachtet werden, wenn Y=5 ⇒ H0. .
Y>5 spricht für H1. Wie groß muß Y sein, damit ihr Zustandekommen unter H0 ’extrem unwahrscheinlich’ ist ? ⇒ Signifikanzniveau α = 0,1 bzw. α = 0,05 oder α = 0,1. .
.
Damit konstruiert man einen Ablehnungsbereich, der alle Werte Y enthält,
Zum Beispiel: n=10; p=0,5; α=0,1; für H0: Y ∼ Binomial(n=10, p=0,5) .
.
Lösung ansehen .
.
Mögliche Fehlentscheidungen .