19.1.3 Chi-Quadrat-Test
.
Wir erweitern den Test mit den Münzwürfen auf ein Würfelspiel: bei einem fairen Würfel tritt jede der sechs möglichen Augenzahlen 1,2..6 mit der gleichen Wahrscheinlichkeit auf: .
pi=1/6 (i=1,2..6) .
Die Frage, ab wann der Würfel im Verdacht steht, nicht mehr als fair zu gelten, könnte analog zu oben mit der Binomialverteilung angegangen werden.
Man trägt zunächst die Häufigkeitswerte in einem Histogramm auf und bestimmt die jeweiligen Differenzen von theoretischen (Wahrscheinlichkeitsfunktion bzw. -Dichte) und beobachteten Häufigkeiten. .
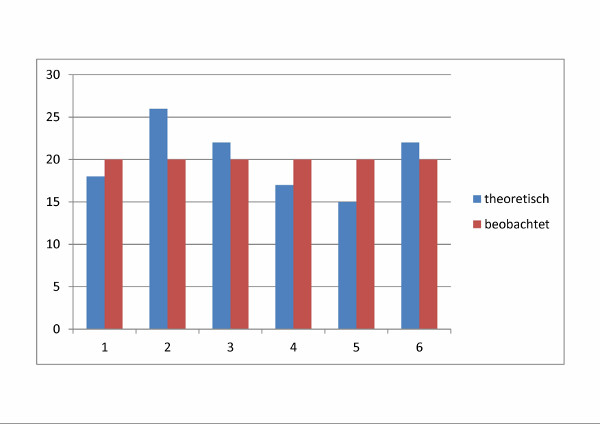
| Abbildung 102: Beispiel für 120 Würfe |
.
| Klasse No. | ni (beobachtet) | pi (theoretisch) | ni*=n· pi (theoretisch) | Δ ni = ni−ni* | Δ ni2 | |
| 1 | n1 | p1 | n1*=n· p1 | n1−n1* | Δ n12 | |
| 2 | n2 | p2 | n2*=n· p2 | n2−n2* | Δ n22 | |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| k | nk | pk | nk*=n· pk | nk−nk* | Δ nk2 | |
| Σ | n | 1 | n | 0 | 0 | χ2 |
.
Beispiel 19 - 20 st9081
Präferenz von Produkten .
Ein Hersteller stellt 4 Sorten von Bier her, nämlich alkoholfrei (A), Pils (B), Export (C) und Weizen (D). .
Ein Marketing-Unternehmen hat eine Befragung von 200 Personen durchgeführt, welche Sorte sie bevorzugen: .
.
| Sorte | Anzahl Nennungen |
| A | 43 |
| B | 53 |
| C | 60 |
| D | Rest |
.
.
Testen Sie für ein Konfidenzintervall von 10 %, ob dies noch als zufällig angesehen werden kann oder nicht. .
(Achtung: sowohl linke (10 %) als auch rechte Seite (90%) zählen !)
.
Lösung ansehen .
.

