20.1.2  Auswertung und Beurteilung einer Messreihe

Wenn man die Anzahl der Messungen in der Messreihe beliebig erhöht, geht die diskrete Häufigkeitsverteilung in eine kontinuierliche (stetige) Verteilung über. In vielen Fällen nimmt man eine normalverteilte Zufallsvariable an und beschreibt die Messgröße X durch die normierte Dichtefunktion .

.
.
.
.
µ : Mittelwert .
σ : Standardabweichung. .

---

Abbildung 104: Normalverteilung mit σ= 1; 0,75; 0,5

---

Wie bereits aufgeführt, gilt für eine normalverteilte Meßreihe: .
Als ’bester’ Schätzwert für den unbekannten ’wahren’ Wert µ der Meßgröße ’X’ gilt der .
arithmetische Mittelwert .
x = 1/n (x₁+x₂+x₃+...+x_n) = 1/n · ∑_i=1ⁿ x_i. .
.
Ein geeignetes Maß für die Streuung der Einzelmessungen x_i ist die Standardabweichung .
.
.
.
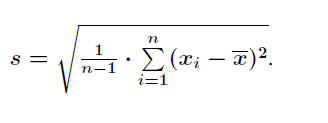Für jeden Mittelwert kann man eine Standardabweichung s _x des Mittelwerts x angeben: .
.
.
.
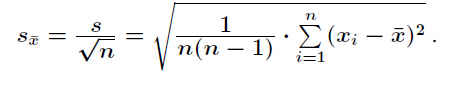Sie beschreibt die Streuung der Mittelwerte (die man aus mehreren Messreihen erhalten hat) um den ’wahren’ Mittelwert µ.