ErklärungenWissen über Eigenschaften und "spezielle Punkte" von Funktionen/ Graphen ist in vielen Fällen sehr nützlich und hilft häufig viel weiter als eine ausführliche Wertetabelle. Weiß man beispielsweise, dass eine Funktion achsensymmetrisch zur y-Achse ist, reicht es aus, die Funktionswerte für nichtnegative x-Werte zu berechen - die entsprechenden Funktionswerte für negative x-Werte erhält man in einem solchen Fall automatisch. "Besondere Punkte" einer FunktionNullstellen und ExtremaDefinition: Eine Funktion 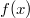 hat an einer Stelle 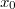 eine Nullstelle, wenn 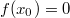 ist. Definition: Eine Funktion 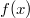 hat an einer Stelle 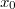 einen Tiefpunkt oder Minimum, wenn der zu 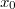 gehörende Funktionswert 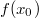 in einer gewissen Umgebung von 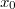 der kleinste Funktionswert ist. Definition: Eine Funktion 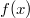 hat an einer Stelle 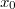 einen Hochpunkt oder Maximum, wenn der zu 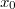 gehörende Funktionswert 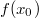 in einer gewissen Umgebung von 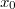 der größte Funktionswert ist. Definition: Eine Funktion hat an einer Stelle 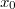 ein Extremum, wenn die Funktion in 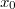 entweder ein Minimum oder ein Maximum hat. Selbstverständlich werden hier nur solche Stellen 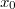 betrachtet, die im Definitionsbereich liegen! In der folgenden Graphik sind die Funktionen 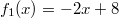 , 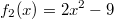 , 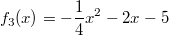 und 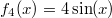 zu sehen (Mehr zur Funktion 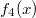 erfahren Sie im Kapitel Trigonometrie). Die Nullstellen sind mit braunen, die Maxima mit dunkelblauen und die Minima mit hellblauen Kreisen markiert. Zur Berechnung von Extremstellen wird in vielen Fällen die Differenzialrechnung benötigt. ACHTUNG: Wie in der folgenden Grafik zu sehen ist, hängt es auch vom Definitionsbereich ab, ob eine Funktion an einer Stelle ein Extremum hat. Die Grafik zeigt die gleichen Funktionen wie zuvor, allerdings mit 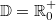 statt 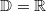 . Alle Extrema im negativen x-Bereich sind weggefallen. Dafür finden sich an der Stelle 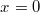 , also am unteren Rand des Definitionsbereiches, nun vier Extrema statt wie vorher nur eines. Wende- und SattelpunkteDefinition: Ein Wendepunkt ist ein Punkt, an dem ein Funktionsgraph sein Krümmungsverhalten ändert - von einer Rechtskrümmung ("Rechtskurve") zu einer Linkskrümmung ("Linkskurve") oder umgekehrt. Definition: Ein Sattelpunkt ist ein Wendepunkt, an dem die Steigung der Funktion 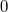 ist, d. h. der Graph der Funktion ist an dieser Stelle horizontal. In der folgenden Grafik sind die Funktionen 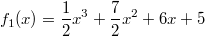 und 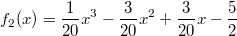 zu sehen. 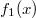 hat einen "normalen" Wendepunkt, 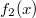 einen Sattelpunkt. Beide sind mit orangefarbenen Kreisen markiert. Wende- und Sattelpunkte lassen sich ohne Differenzialrechnung nicht exakt ermitteln. Dieser Teil der Mathematik ist aber nicht mehr Inhalt des Brückenkurses. PolstelleDefinition: Eine Polstelle ist eine Definitionslücke einer Funktion, in deren Umgebung die Funktionswerte beliebig groß oder beliebig klein werden. In der folgenden Grafik ist die Funktion 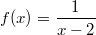 zu sehen. Da durch 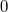 nicht geteilt werden darf, hat die Funktion eine Definitionslücke bei 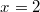 oder - anders formuliert - ihr Definitionsbereich ist 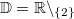 . Im Intervall 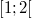 sind die Funktionswerte beliebig klein, während sie im Intervall ![]2;3]](./teximg/img1289.png) beliebig groß sind. Eigenschaften von FunktionenRandverhaltenSymmetrieDefinition: Eine Funktion 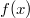 ist achsensymmetrisch zur y-Achse, wenn gilt: 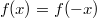 Definition: Definition: Eine Funktion 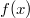 ist punktsymmetrisch zum Koordinatenursprung, wenn gilt: 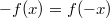 In der folgenden Grafik sind die Funktionen 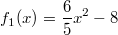 und 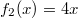 zu sehen. 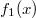 ist achsensymmetrisch zur y-Achse und 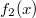 punktsymmetrisch zum Koordinatenursprung. Eine Funktion kann auch zu anderen Geraden außer der y-Achse bzw. zu anderen Punkten außer dem Koordinatenursprung symmetrisch sein. Beispielsweise ist die Funktion 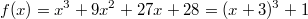 punktsymmetrisch zum Punkt 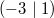 (siehe folgende Grafik). MonotonieDefinition: Eine Funktion 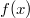 heißt streng monoton steigend, wenn für alle 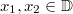 mit 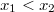 gilt: 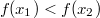 Anders formuliert: Ist 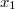 kleiner als 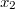 , muss auch der zu 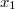 gehörende Funktionswert 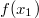 kleiner sein als der Funktionswert, der zu 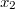 gehört, also 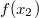 Definition: Definition: Eine Funktion 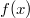 heißt monoton steigend, wenn für alle 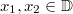 mit 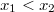 gilt: 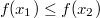 Anders formuliert: Ist 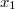 kleiner als 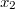 , muss der zu 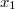 gehörende Funktionswert 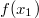 kleiner sein als der Funktionswert, der zu 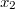 gehört, also 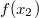 . 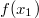 und 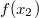 dürfen aber auch identisch sein. Definition: Eine Funktion 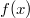 heißt streng monoton fallend, wenn für alle 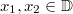 mit 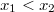 gilt: 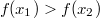 Anders formuliert: Ist 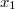 kleiner als 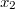 , muss der zu 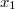 gehörende Funktionswert 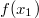 größer sein als der Funktionswert, der zu 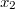 gehört, also 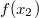 Definition: Definition: Eine Funktion 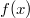 heißt monoton fallend, wenn für alle 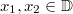 mit 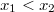 gilt: 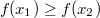 Anders formuliert: Ist 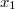 kleiner als 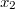 , muss der zu 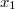 gehörende Funktionswert 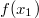 größer sein als der Funktionswert, der zu 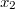 gehört, also 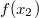 . 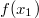 und 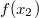 dürfen aber auch identisch sein. In der folgenden Grafik sind die Funktionen 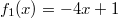 und 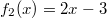 zu sehen. 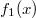 ist streng monoton fallend und 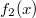 streng monoton steigend.
|
|
 Brückenkurs
Brückenkurs