ErklärungenWas ist ein Bruch?Bei einem Bruch 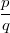 heißt 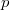 Zähler Zähler und 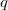 Nenner Nenner. Der Bruchstrich steht dabei für eine Division. Auch wenn für 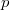 und 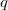 grundsätzlich beliebige reelle Zahlen eingesetzt werden dürfen, ist es üblich, in Brüchen ganze Zahlen zu verwenden, also 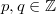 . Immer gilt, dass der Nenner 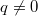 sein muss, da durch 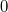 nicht geteilt werden darf! Aufgrund der Rechenregeln für die Division gilt: -
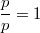 für alle Zahlen für alle Zahlen 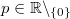
Man unterscheidet folgende Arten von Brüchen: - Echte Brüche: Bei echten Brüchen ist der Betrag der Zählers kleiner als der Betrag des Nenners, d. h. der Betrag des gesamten Bruches ist kleiner als
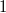 , z. B. , z. B.  - Unechte Brüche: Bei unechten Brüchen ist der Betrag der Zählers größer als der Betrag des Nenners, d. h. der Betrag des gesamten Bruches ist größer als
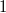 , z. B. , z. B. 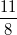
- Gleichnamige Brüche: Brüche, die den gleichen Nenner haben, heißen gleichnamig. Der entsprechende Nenner heißt Hauptnenner der Brüche. Z. B. sind die Brüche
 und und  gleichnamig. Ihr Hauptnenner ist gleichnamig. Ihr Hauptnenner ist 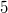 - Ungleichnamige Brüche: Brüche, die nicht den gleichen Nenner haben, heißen ungleichnamig, z. B. sind die Brüche
 und und  ungleichnamig. ungleichnamig.
- Gemischte Zahlen: Gemischte Zahlen bestehen aus einer ganzen Zahl und einem echten Bruch, z. B.
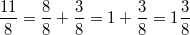 oder oder 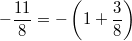 . Wichtig: Bitte beachten Sie, dass die ganze Zahl und der Bruch addiert werden, auch wenn das Pluszeichen weggelassen wird! Normalerweise werden in der Mathematik ausschließlich Malzeichen nicht geschrieben, wenn die Formel etc. trotz des Weglassens eindeutig bleibt. Dies hier ist die große Ausnahme. Da das in vielen Fällen zu Verwirrung führt, sollte diese Schreibweise nur verwendet werden, wenn es dafür wichtige Gründe, z. B. Einschätzen der Größenordnung, gibt. Im Übrigen werden gemischte Zahlen auch nicht benötigt. Echte und unechte Brüche reichen vollkommen aus, um alle Brüche abzubilden. Statt einen unechten Bruch in eine gemischte Zahl umzuwandeln, ist es üblicherweise besser, ihn einfach so stehen zu lassen. . Wichtig: Bitte beachten Sie, dass die ganze Zahl und der Bruch addiert werden, auch wenn das Pluszeichen weggelassen wird! Normalerweise werden in der Mathematik ausschließlich Malzeichen nicht geschrieben, wenn die Formel etc. trotz des Weglassens eindeutig bleibt. Dies hier ist die große Ausnahme. Da das in vielen Fällen zu Verwirrung führt, sollte diese Schreibweise nur verwendet werden, wenn es dafür wichtige Gründe, z. B. Einschätzen der Größenordnung, gibt. Im Übrigen werden gemischte Zahlen auch nicht benötigt. Echte und unechte Brüche reichen vollkommen aus, um alle Brüche abzubilden. Statt einen unechten Bruch in eine gemischte Zahl umzuwandeln, ist es üblicherweise besser, ihn einfach so stehen zu lassen.
DezimalzahlenTeilt man den Zähler eines Bruches durch seinen Nenner, erhält man eine Dezimalzahl, auch "Kommazahl" genannt, z. B. 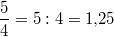 Auch bei den Dezimalzahlen unterscheidet man verschiedene "Sorten": - Endliche Dezimalzahlen: Eine Dezimalzahl mit endlich vielen Nachkommastellen, z. B.
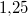 oder oder 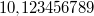 - Unendliche Dezimalzahlen: Eine Dezimalzahl mit unendlich vielen Nachkommastellen. Hier unterscheidet man weiter:
- Periodische Dezimalzahlen: Bei periodischen Dezimalzahlen wiederholt sich innerhalb der unendlichen Folge von Nachkommastellen ein bestimmtes Muster immer wieder, z. B.
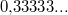 oder oder 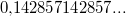 oder oder 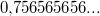 Dies macht man kenntlich, indem man nur das erste Auftreten dieser Periode notiert - mit einem horizontalen Strich darüber, z. B. Dies macht man kenntlich, indem man nur das erste Auftreten dieser Periode notiert - mit einem horizontalen Strich darüber, z. B. 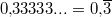 oder oder 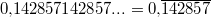 oder oder 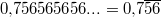 . Dann benötigt man keine Pünktchen mehr dahinter. Sie sollen ja nur andeuten, dass die Zahl unendlich weitergeht und nicht nach den angegeben Nachkommastellen aufhört. Der (mathematische) Unterschied zwischen . Dann benötigt man keine Pünktchen mehr dahinter. Sie sollen ja nur andeuten, dass die Zahl unendlich weitergeht und nicht nach den angegeben Nachkommastellen aufhört. Der (mathematische) Unterschied zwischen 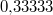 und und 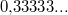 ist zwar nicht groß, aber er ist da... ist zwar nicht groß, aber er ist da... - Nichtperiodische Dezimalzahlen: Nichtperiodische Dezimalzahlen haben kein solches Muster in ihrer unendlichen Folge von Nachkommastellen, z. B.
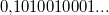 oder oder 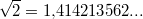 oder oder 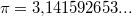 (die beiden letzten Beispiele werden Sie in den Kapiteln "Potenzen, Wurzeln, Logarithmen" bzw. "Geometrie" kennen lernen). Wichtig ist auch hier, dass die drei kleinen Pünktchen am Ende nicht vergessen werden. Benötigt man nur eine bestimmte Anzahl von Nachkommastellen (was ja meistens der Fall ist), muss entsprechend gerundet werden. (die beiden letzten Beispiele werden Sie in den Kapiteln "Potenzen, Wurzeln, Logarithmen" bzw. "Geometrie" kennen lernen). Wichtig ist auch hier, dass die drei kleinen Pünktchen am Ende nicht vergessen werden. Benötigt man nur eine bestimmte Anzahl von Nachkommastellen (was ja meistens der Fall ist), muss entsprechend gerundet werden.
Rechenregeln für BrücheErweiternZwei Brüche werden erweitert, indem man Zähler und Nenner mit der gleichen Zahl multipliziert. Der Wert des Bruches ändert sich dabei nicht. Z. B. 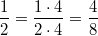 KürzenZwei Brüche werden gekürzt, indem man Zähler und Nenner durch die gleiche Zahl dividiert. Der Wert des Bruches ändert sich dabei nicht. Z. B. 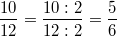 Es versteht sich (eigentlich) von selbst, dass 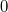 keine geeignete Zahl zum Erweitern oder Kürzen ist, weil man ja nun mal durch 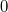 nicht teilen darf... AdditionZwei gleichnamige Brüche werden addiert, indem man die Zähler addiert und den Nenner unverändert lässt. Z. B. 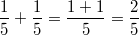 Zwei ungleichnamige Brüche werden addiert, indem man sie gleichnamig macht (z. B. durch Erweitern) und dann addiert. Z. B. 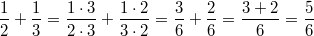 SubtraktionZwei gleichnamige Brüche werden subtrahiert, indem man die Zähler subtrahiert und den Nenner unverändert lässt. Z. B. 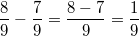 Zwei ungleichnamige Brüche werden subtrahiert, indem man sie gleichnamig macht (z. B. durch Erweitern) und dann subtrahiert. Z. B. 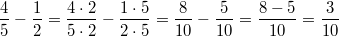 MultiplikationZwei Brüche werden multipliziert, indem man jeweils die Zähler und die Nenner multipliziert. Z. B. 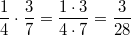 DivisionZwei Brüche werden dividiert, indem man mit dem Kehrwert des zweiten Bruches multipliziert. Z. B. 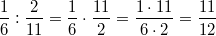 Bemerkung: Ist das Ergebnis einer Bruchrechnungsaufgabe ein Bruch, sollte dieser so weit wie möglich gekürzt werden. Abhängig von der Aufgabenstellung (z. B. wenn die Größenordnung von Bedeutung ist) kann es sinnvoll sein, das Ergebnis als gemischte Zahl darzustellen. Bei Multiplikationsaufgaben und damit auch bei Divisionsaufgaben sollte immer vor dem Multiplizieren überprüft werden, ob die Brüche gegeneinander gekürzt werden können. Je früher in einer Rechnung gekürzt wird, desto handlicher bleibt die Aufgabe. ACHTUNG: Aus Summen darf man nicht kürzen! |
|
 Brückenkurs
Brückenkurs