Ein lineares Gleichungssystem ist ein System, das aus mehreren linearen Gleichungen besteht, die zusammen gelöst werden sollen. Das bedeutet, dass Zahlen gesucht werden, die gleichzeitig Lösung von allen Gleichungen des Systems sind. Grundsätzlich ist die Zahl der Gleichungen und Variablen nicht beschränkt. Wir beschäftigen uns hier allerdings vorrangig mit linearen Gleichungssystemen, die zwei lineare Gleichungen und zwei Variablen enthalten.

Der Definitionsbereich wird bei linearen Gleichungssystemen mit zwei Variablen so notiert: 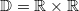. Das gibt an, dass zwei Zahlen gesucht sind und diese Zahlen beide den reellen Zahlen entstammen sollen.
Die Lösung (so vorhanden) besteht in diesem Fall auch aus zwei Zahlen, nämlich für jede Variable eine. Genauer gesagt besteht die Lösung aus einem geordneten Zahlenpaar (oder auch 2-Tupel), das folgendermaßen notiert wird: 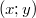. Wichtig ist natürlich, dass diese beiden Zahlen nicht vertauscht werden. Schreibt man solche Lösungen in eine Lösungsmenge bleiben die runden Klammern erhalten, um die Anordnung festzuhalten: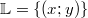

Bei linearen Gleichungssystemen mit mehr als zwei Variablen und Gleichungen werden diese Notationen entsprechend erweitert.

Lineare Gleichungssysteme können keine, eine oder unendlich viele Lösungen haben, d. h. sie können nicht, eindeutig oder mehrdeutig (und dann mit unendlich vielen Lösungen) lösbar sein. Da lineare Gleichungssysteme nun mal aus linearen Gleichungen bestehen, benötigen wir hier keine neuen Überlegungen, was die Lösbarkeit angeht. Wir können stattdessen ausnutzen, dass wir uns diese Gedanken bereits im Kapitel lineare Gleichungen gemacht haben. Die beste Voraussetzung für eine eindeutige Lösung ist, ein lineares Gleichungssystem mit genauso vielen Gleichungen wie Variablen.

Wichtige Verfahren zum Lösen linearer Gleichungssysteme sind: das Additionsverfahren, das Gleichsetzungsverfahren und das Einsetzungsverfahren. Häufig ist auch eine grafische Lösung möglich. Grundsätzlich liefern alle Verfahren dasselbe Ergebnis, wenn man sie auf dasselbe lineare Gleichungssystem anwendet. Der Lösungsweg kann allerdings u. U. etwas länger und umständlicher werden, wenn man nicht den geschicktesten Weg wählt.

Primäres Ziel der Verfahren ist es, das lineare Gleichungssystem so umzuformen, dass in einer der Zeilen nur noch eine Variable vorhanden ist, da lineare Gleichungen mit einer Variablen (wie wir ja schon gesehen haben) leicht gelöst werden können.

Für alle drei genannten Verfahren gilt: Die Lösungsmenge des Gleichungssystems darf sich während der Anwendung nicht ändern, sonst wären die Zahlen, die man berechnet, ja nicht Lösungen des Gleichungssystems. Es müssen also Äquivalenzumformungen verwendet werden. Zu den Äquivalenzumformungen, die für lineare Gleichungen grundsätzlich gelten, kommen hier noch weitere hinzu. Im Einzelnen sind dies:

• die Addition von einer Zeile des linearen Gleichungssystems zu einer anderen Zeile
• das Vertauschen von zwei Zeilen des linearen Gleichungssystems

Zur Notation: Die Angaben am Ende einer Gleichung hinter dem senkrechten Strich geben wieder an, welche Rechenoperationen auf diese Zeile des Gleichungssystems angewendet werden. Mit der Nummerierung der Gleichungen deutet man an, welche Gleichungen zusammengerechnet werden.

Idee: Die einzelnen Gleichungen werden mit entsprechenden Zahlen so multipliziert, dass die Koeffizienten vor einer der Variablen Gegenzahlen sind. Dann können die Gleichungen addiert werden mit der Folge, dass diese Variable den Koeffizienten 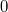hat, also wegfällt. Es bleibt (im Allgemeinen) eine Gleichung mit einer Variablen übrig, die dann gelöst werden kann. Der so erhaltene Wert für die Variable wird in eine der Ausgangsgleichungen eingesetzt, damit die andere Variable berechnet werden kann.

Beispiel: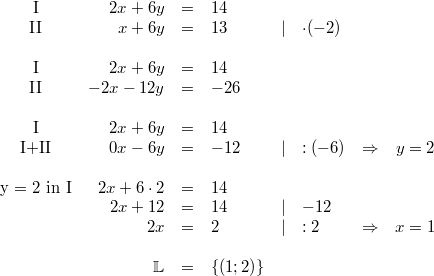

Idee: Hat eine Variable in beiden Gleichungen denselben Koeffizienten, kann man diese Tatsache ausnutzen, indem man diese gleichen Summanden in ihren Gleichungen isoliert. Sprich: Man formt die Gleichungen so um, dass die gleichen Summanden alleine z. B. auf den linken Seiten der Gleichungen stehen. Man folgert: Sind die linken Seiten der beiden Gleichungen gleich, müssen es auch die rechten sein. Man kann diese also gleichsetzen. Auf den beiden rechten Seiten ist aber nur noch eine Variable enthalten, sodass man im Normalfall eine lineare Gleichung mit einer Variablen erhält. Diese löst man und setzt den erhaltenen Zahlenwert in einer der Ausgangsgleichungen ein, um die andere Variable zu berechnen.

Beispiel: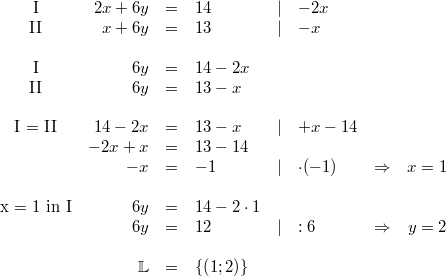

Idee: Dieses Verfahren bietet sich an, wenn eine Variable in einer Gleichung den Koeffizienten 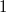hat. (Hinweis: Den Koeffizienten 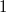notiert man häufig nicht!) Man formt die Gleichung so um, dass die Variable mit dem Koeffizienten 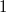alleine auf einer Seite der Gleichung steht. Dann hat man eine Möglichkeit gefunden, diese Variable mithilfe der anderen auszudrücken. Diese Umschreibung der Variablen kann man in die andere Gleichung einsetzen (Hinweis: Häufig sind hier Klammern nötig!) und erhält normalerweise eine Gleichung, die nur noch eine Variable enthält. Wenn man diese gelöst hat, setzt man den gefundenen Wert in die erste Gleichung ein und kann so auch für die zweite Variable einen Wert berechnen.

Beispiel: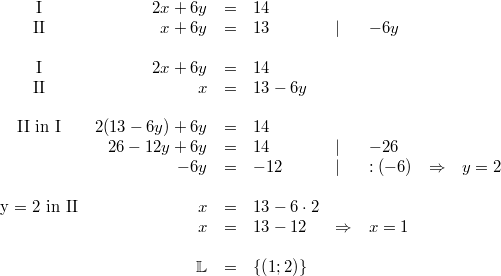

Bei der grafischen Lösung eines linearen Gleichungssystems fasst man die einzelnen linearen Gleichungen als lineare Funktionen auf. Evtl. muss man sie dafür ein wenig umformen, sodass sie in der Form 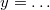vorliegen. Anschließend kann man sie in ein Koordinatensystem eintragen und den Schnittpunkt bestimmen. Dieser ist die gesuchte Lösung.

Natürlich gibt es auch lineare Gleichungssysteme mit mehr Gleichungen und Variablen. Diese sind (natürlich) aufwändiger zu lösen. Die gute Nachricht: Am Prinzip ändert sich nichts. Wenn Sie also verstanden haben, wie man lineare Gleichungssysteme mit zwei Gleichungen und zwei Variablen löst, wissen Sie auch, wie man lineare Gleichungssysteme mit zehn Gleichungen und zehn Variablen löst. Dass man das meist nicht mehr mit Stift und Papier machen möchte, ist eine andere Sache...
Hier ein Beispiel eines linearen Gleichungssystems mit drei Gleichungen und drei Variablen:

Hinweis: Bitte beachten Sie, dass die Rechenoperationen hier nicht mehr hinter die Gleichungen geschrieben, sondern in die Nummerierung integriert wurden. Das hat den Grund, dass beim ersten Schritt Gleichung I einmal mit 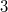und einmal mit 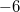multipliziert werden muss, damit bei der Addition der Gleichungszeilen das entsprechende Element in den Zeilen II bzw. III wegfällt. Das alles hinter die Gleichung zu schreiben, wäre zu viel und unübersichtlich. Ein Strich hinter einer Zeilennummer (z. B. II') deutet an, dass es sich zwar noch um Gleichung II handelt, mit dieser Gleichung aber schon Berechnungen vorgenommen wurden. Es ist also nicht mehr die Originalgleichung.

Für den Definitionsbereich gilt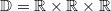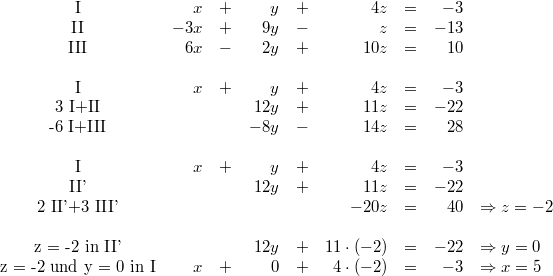



Die Lösungsmenge lautet also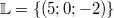

Sie haben vielleicht bemerkt, dass der Lösungsweg eine Erweiterung des oben beschriebenen Additionsverfahrens ist. Bei linearen Gleichungssystemen mit mehr als zwei Gleichungen und Variablen entscheidet man sich meist dafür (und nicht für das Gleichsetzungs- oder Einsetzungsverfahren), weil das Gleichungssystem damit überschaubarer bleibt - aber auch weil dieser Rechenweg die Grundlage für das wohl bekannteste Lösungsverfahren in diesem Zusammenhang ist: Das gaußsche Eliminationsverfahren, benannt nach Carl Friedrich Gauß, welches auch deswegen von so großer Bedeutung ist, weil es sich gut in Computerprogrammen abbilden lässt. Damit ist gesichert, dass wir lineare Gleichungssysteme mit zehn Gleichungen und zehn Variablen tatsächlich nicht mehr mit Stift und Papier lösen müssen.