Brotkrumen-Navigation

Brückenkurs » 8 Potenzen, Wurzeln, Logarithmen

Brückenkurs

Erklärungen

Aufgaben

Lösungen

1. Aufgabe

Hinweis 1: Über die Teilbarkeitsregeln können Basen ausgeschlossen werden. Z. B. ist 121

nicht durch

und

teilbar. Erst die

kommt überhaupt als Basis infrage.
Hinweis 2: Das Erkennen von Quadratzahlen ist in vielen Fällen, so auch hier, sehr nützlich.

1) 400=20^2

2. Aufgabe

1) $2\sqrt{x} + 3\sqrt{x} = 5\sqrt{x}$

2) $2\sqrt{x} - 3\sqrt{x} = -1\sqrt{x} = -\sqrt{x}$
Bemerkung: Addition und Subtraktion wirken auf Koeffizienten nicht auf Exponenten.

3) $2\sqrt{x} \cdot 3\sqrt{x} = 6x$

4) $2\sqrt{x} : 3\sqrt{x} = \frac{2}{3} x$
Bemerkung: $2\sqrt{x} : 3\sqrt{x} = 2\sqrt{x} : 3 \cdot \sqrt{x} \quad \neq \quad 2\sqrt{x} : \left(3\sqrt{x}\right) = \frac{2}{3}$ . Diese Unterscheidung ist vor allem bei der Arbeit mit dem Taschenrechner wichtig!

3. Aufgabe

Variablenwerte müssen ausgeschlossen werden, wenn

der Nenner für diesen Wert / diese Werte 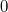wird,
der Radikand für diesen Wert / diese Werte negativ wird,
das Logarithmusargument für diesen Wert / diese Werte negativ oder 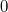wird bzw.
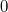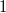die Basis eines Logarithmus' für diesen Wert / diese Werte negativ, oder ist.

Egal, wie komplex die folgenden Aufgaben werden, es gelten immer die fundamentalen Rechenregeln, wie "Punkt vor Strich", Klammergesetze, die Gesetze der Bruchrechnung etc.

1)
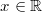
Für alle $x\in \mathbb{R}$ gilt:
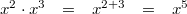$\begin{array}{rcccl} x^2 \cdot x^3 &=& x^{2+3} &=& x^5\end{array}$

Vorgehen: 1. Potenzgesetz

2)
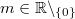
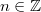
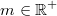
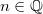
Für alle $m \in \mathbb{R}\backslash_{\{0\}}$ und $n \in \mathbb{Z}$ oder für alle $m\in \mathbb{R}^+$ und $n\in \mathbb{Q}$ gilt:
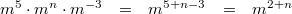$\begin{array}{rcccl} m^5 \cdot m^n \cdot m^{-3} &=& m^{5+n-3} &=& m^{2+n}\end{array}$

Vorgehen: 1. Potenzgesetz

3)
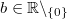
Für alle $b \in \mathbb{R}\backslash_{\{0\}}$ gilt:
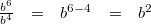$\begin{array}{rcccl} \frac{b^6}{b^4} &=& b^{6-4} &=& b^2\end{array}$

Vorgehen: 2. Potenzgesetz

4)
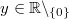
Für alle $y \in \mathbb{R}\backslash_{\{0\}}$ gilt:
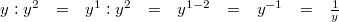$\begin{array}{rcccccccl}y : y^2 &=& y^1 : y^2 &=& y^{1-2} &=& y^{-1} &=& \frac{1}{y}\end{array}$

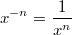
Vorgehen: 2. Potenzgesetz, Festlegung: $x^{-n}=\frac{1}{x^n}$

5)
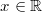
Für alle $x\in \mathbb{R}$ gilt:
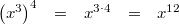$\begin{array}{rcccl} \left(x^3\right)^4 &=& x^{3 \cdot 4} &=& x^{12}\end{array}$

Vorgehen: 3. Potenzgesetz

6)
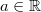
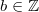
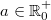
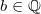
Für alle $a\in \mathbb{R}$ und $b\in \mathbb{Z}$ oder für alle $a\in \mathbb{R}^+_0$ und $b\in \mathbb{Q}$ gilt:
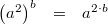$\begin{array}{rcl}\left(a^2\right)^b &=& a^{2 \cdot b}\end{array}$

Vorgehen: 3. Potenzgesetz
Bemerkung: Ist

negativ oder

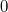
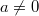
, muss zusätzlich $a\neq 0$ gelten.

7)
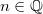
Für alle $n\in \mathbb{Q}$ gilt:
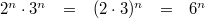$\begin{array}{rcccl}2^n \cdot 3^n &=& (2 \cdot 3)^n &=& 6^n \end{array}$

Vorgehen: 4. Potenzgesetz

8)
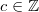
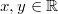
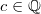
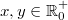
Für alle $c\in \mathbb{Z}$ und $x,y\in \mathbb{R}$ oder für alle $c\in \mathbb{Q}$ und $x,y\in \mathbb{R}^+_0$ gilt:
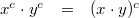$\begin{array}{rcl} x^c \cdot y^c &=& (x \cdot y)^c\end{array}$

Vorgehen: 4. Potenzgesetz
Bemerkung: Ist

negativ oder

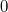
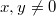
, muss zusätzlich $x,y \neq 0$ gelten.

9)
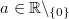
Für alle $a \in \mathbb{R}\backslash_{\{0\}}$ gilt:
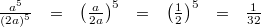$\begin{array}{rcccccl}\frac{a^5}{(2a)^5} &=& \left( \frac{a}{2a}\right)^5 &=& \left(\frac{1}{2}\right)^5 &=& \frac{1}{32}\end{array}$

Vorgehen: 5. Potenzgesetz

10)
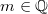
Für alle $m\in \mathbb{Q}$ gilt:
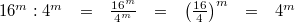$\begin{array}{rcccccl}16^m : 4^m &=& \frac{16^m}{4^m} &=& \left(\frac{16}{4}\right)^m &=& 4^m \end{array}$

Vorgehen: 5. Potenzgesetz

11)
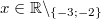
Für alle $x \in \mathbb{R}\backslash_{\{-3;-2\}}$ gilt:
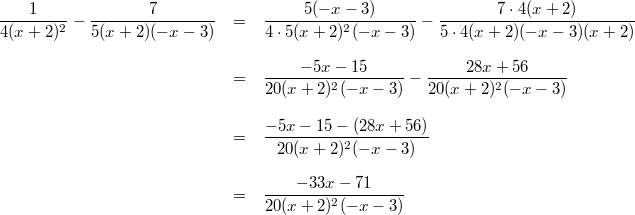$\begin{array}{ccl} \dfrac{1}{4(x+2)^2}-\dfrac{7}{5(x+2)(-x-3)} &=& \dfrac{5(-x-3)}{4 \cdot 5(x+2)^2(-x-3)}-\dfrac{7 \cdot 4 (x+2)}{5 \cdot 4(x+2)(-x-3)(x+2)} \\ \\ &=& \dfrac{-5x-15}{20(x+2)^2(-x-3)}-\dfrac{28x+56}{20(x+2)^2(-x-3)} \\ \\ &=& \dfrac{-5x-15-(28x+56)}{20(x+2)^2(-x-3)} \\ \\ &=& \dfrac{-33x-71}{20(x+2)^2(-x-3)} \end{array}$

Vorgehen: Brüche gleichnamig machen und zusammenfassen
Bemerkung: Man könnte noch im Nenner die Klammern ausmultiplizieren.

12)
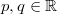
Für alle $p,q \in \mathbb{R}$ gilt:
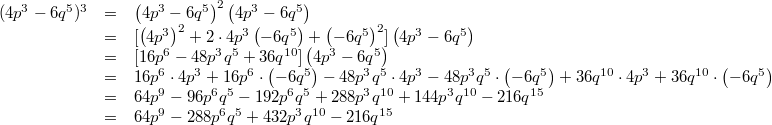$\begin{array}{ccl} (4p^3-6q^5)^3 &=& \left(4p^3-6q^5 \right)^2 \left(4p^3-6q^5 \right) \\ &=& \lbrack \left(4p^3 \right)^2 + 2 \cdot 4p^3 \left(-6q^5 \right)+\left(-6q^5 \right)^2 \rbrack \left(4p^3-6q^5 \right) \\ &=& \lbrack 16p^6-48p^3q^5+36q^{10}\rbrack \left(4p^3-6q^5 \right) \\ &=& 16p^6 \cdot 4p^3 + 16p^6 \cdot \left(-6q^5 \right) - 48 p^3q^5 \cdot 4p^3 - 48 p^3q^5 \cdot \left(-6q^5 \right) + 36 q^{10} \cdot 4p^3 + 36 q^{10} \cdot \left(-6q^5 \right) \\ &=& 64p^9-96p^6q^5-192p^6q^5+288p^3q^{10}+144p^3q^{10}-216q^{15} \\ &=& 64p^9-288p^6q^5+432p^3q^{10}-216q^{15} \end{array}$

Vorgehen: 2. Binomische Formel, ausmultiplizieren, 3. und 4. Potenzgesetz
Bemerkung 1: Werden in einer Rechnung viele Klammern ineinander verschachtelt benötigt, kann man zur besseren Übersicht auch eckige oder geschweifte Klammern verwenden.
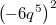
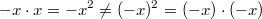
Bemerkung 2: Achten Sie darauf, dass z. B. bei $\left(-6q^5\right)^2$ Klammern gesetzt werden müssen. Insbesondere gehört auch das Minuszeichen mit in die Klammer, da gilt $-x\cdot x = -x^2 \neq (-x)^2 = (-x) \cdot (-x)$

13)
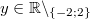
Für alle $y \in \mathbb{R}\backslash_{\{-2;2\}}$ gilt:
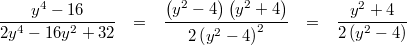$\begin{array}{rcccl}\dfrac{y^4-16}{2y^4-16y^2+32} &=& \dfrac{ \left(y^2-4 \right) \left(y^2+4 \right)}{2\left(y^2-4 \right)^2} &=& \dfrac{y^2+4}{2\left(y^2-4\right)}\end{array}$

Vorgehen: Binomische Formeln "rückwärts", kürzen
Bemerkung: Sie erkennen die 3. Binomische Formel im Zähler daran, dass zwei Terme, die jeweils für sich quadratisch sind, voneinander subtrahiert werden. Im Nenner gibt es zwei quadratische Terme mit jeweils positivem Vorzeichen sowie einen gemischten Term. Solch eine Konstellation ist ein guter Kandidat für die Anwendung der 1. oder 2. Binomischen Formel. Es kann aber sein, dass sie sich nicht in dieser Weise umformen lässt, wenn nämlich der gemischte Term nicht zu den beiden quadratischen passt.

14)
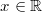
Für alle $x\in \mathbb{R}$ gilt:
$\begin{array}{rcl} 5e^{-x+1}-2xe^{-x+1} &=& (5-2x)e^{-x+1}\end{array}$

Vorgehen: ausklammern

15)
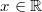
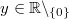
Für alle $x \in \mathbb{R}$ und $y \in \mathbb{R}\backslash_{\{0\}}$ gilt:
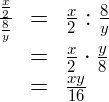$\begin{array}{ccl} \Large\frac{\frac{x}{2}}{\frac{8}{y}} &=& \frac{x}{2} : \frac{8}{y} \\ &=& \frac{x}{2} \cdot \frac{y}{8} \\ &=& \frac{xy}{16} \end{array}$

Vorgehen: Mit dem Kehrwert des Nennerbruches multiplizieren
Bemerkung: Dieses Vorgehen ist für die Umformung von Doppelbrüchen grundsätzlich empfehlenswert.

16)
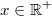
Für alle $x \in \mathbb{R}^+$ gilt:
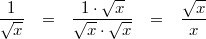$\begin{array}{ccccl} \dfrac{1}{\sqrt{x}} &=& \dfrac{1 \cdot \sqrt{x}}{\sqrt{x} \cdot \sqrt{x}} &=& \dfrac{\sqrt{x}}{x} \end{array}$

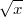Vorgehen: erweitern mit $\sqrt{x}$
Bemerkung 1: Mit einer Wurzel im Nenner rechnet es sich meist nicht sehr gut. Daher erweitert man solche Brüche so, dass der Nenner rational wird.
Bemerkung 2: Eine ganz ähnliche Vorgehensweise wird bei der Division komplexer Zahlen, z. B. in der Elektrotechnik, benötigt.

17)
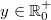
Für alle $y \in \mathbb{R}^+_0$ gilt:
$\begin{array}{ccl} \left(y^{\frac{1}{3}}\right)^2 &=& y^{\frac{1}{3} \cdot 2} \\ &=& y^{\frac{2}{3}} \\ &=& \sqrt [3]{y^2} \end{array}$

Vorgehen: 3. Potenzgesetz, Potenz in Wurzelschreibweise umformen

18)
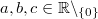
Für alle $a,b,c \in \mathbb{R}\backslash_{\{0\}}$ gilt:
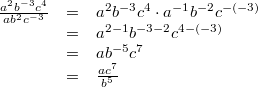$\begin{array}{ccl} \frac{a^2b^{-3}c^4}{ab^2c^{-3}} &=& a^2b^{-3}c^4 \cdot a^{-1}b^{-2}c^{-(-3)} \\ &=& a^{2-1}b^{-3-2}c^{4-(-3)} \\ &=& ab^{-5}c^7 \\ &=& \frac{ac^7}{b^5} \end{array}$

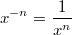
Vorgehen: Festlegung: $x^{-n}=\frac{1}{x^n}$ , 1. Potenzgesetz

19)
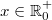
Für alle $x \in \mathbb{R}^+_0$ gilt:
$\begin{array}{ccl} \sqrt[3]{x} \cdot \sqrt{x} &=& x^{\frac{1}{3}} \cdot x^{\frac{1}{2}} \\ &=& x^{\frac{1}{3} + \frac{1}{2}} \\ &=& x^{\frac{5}{6}} \\ &=& \sqrt [6]{x^5} \end{array}$

Vorgehen: Wurzeln in Potenzschreibweise, 1. Potenzgesetz

20)
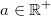
Für alle $a \in \mathbb{R}^+$ gilt:
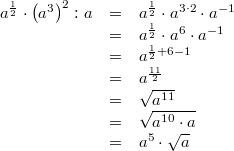$\begin{array}{ccl} a^{\frac{1}{2}} \cdot \left(a^3\right)^2 : a &=& a^{\frac{1}{2}} \cdot a^{3 \cdot 2} \cdot a^{-1} \\ &=& a^{\frac{1}{2}} \cdot a^6 \cdot a^{-1} \\ &=& a^{\frac{1}{2}+6-1} \\ &=& a^{\frac{11}{2}} \\ &=& \sqrt{a^{11}} \\ &=& \sqrt{a^{10} \cdot a} \\ &=& a^5 \cdot \sqrt{a} \end{array}$

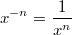
Vorgehen: 3. und 1. Potenzgesetz, Festlegung: $x^{-n}=\frac{1}{x^n}$ , Potenz in Wurzelschreibweise umformen
Bemerkung: Die Umformung vom vorletzten zum letzten Term nennt man "teilweises Wurzelziehen".

21)
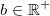
Für alle $b\in \mathbb{R}^+$ gilt:
$\begin{array}{ccl} \frac{ \sqrt[5]{b^3}}{b} &=& b^{\frac{3}{5}} \cdot b^{-1} \\ &=& b^{\frac{3}{5}-1} \\ &=& b^{-\frac{2}{5}} \\ &=& \frac{1}{\sqrt [5]{b^2}} \end{array}$

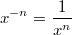
Vorgehen: Wurzel in Potenzschreibweise, Festlegung: $x^{-n}=\frac{1}{x^n}$ , 1. Potenzgesetz, Potenz wieder in Wurzelschreibweise

22)
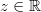
Für alle $z\in \mathbb{R}$ gilt:
$\begin{array}{ccl} \left( \sqrt[4]{z^2}\right)^3 &=& \left( z^{\frac{2}{4}} \right)^3 \\ &=& \vert z \vert^{\frac{1}{2} \cdot 3} \\ &=& \vert z \vert^{\frac{3}{2}} \\ &=& \sqrt{\vert z \vert^3} \end{array}$

Vorgehen: Wurzel in Potenzschreibweise umformen und wieder zurück, zwischendurch 3. Potenzgesetz
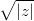
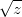
Bemerkung: Bitte beachten Sie: $\sqrt[4]{z^2}=\sqrt{\vert z \vert}$ , da es sonst Schwierigkeiten bei negativen Zahlen gibt. Bei $\sqrt[4]{z^2}$ und $\sqrt{\vert z \vert}$ dürfen sie eingesetzt werden - bei $\sqrt{z}$ nicht.

23)
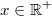
Für alle $x \in \mathbb{R}^+$ gilt:
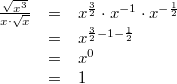$\begin{array}{ccl} \frac{ \sqrt{x^3}}{x \cdot \sqrt{x}} &=& x^{\frac{3}{2}} \cdot x^{-1} \cdot x^{-\frac{1}{2}} \\ &=& x^{\frac{3}{2}-1-\frac{1}{2}} \\ &=& x^0 \\ &=& 1 \end{array}$

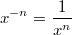
Vorgehen: Wurzel in Potenzschreibweise, Festlegung: $x^{-n}=\frac{1}{x^n}$ , 1. Potenzgesetz, Festlegung: x^0=1

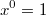
24)
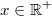
Für alle $x \in \mathbb{R}^+$ gilt:
$\begin{array}{ccl} \left( \frac{1}{x^2} \cdot x^{-2} \right)^2 \cdot \sqrt[2]{x} &=& \left( x^{-2} \cdot x^{-2} \right)^2 \cdot x^{\frac{1}{2}} \\ &=& \left( x^{-2-2} \right)^2 \cdot x^{\frac{1}{2}} \\ &=& x^{-4 \cdot 2} \cdot x^{\frac{1}{2}} \\ &=& x^{-8+\frac{1}{2}} \\ &=& x^{-\frac{15}{2}} \\ &=& \dfrac{1}{\sqrt{x^{15}}} \\ &=& \dfrac{1}{x^7 \cdot \sqrt{x}} \\ &=& \dfrac{\sqrt{x}}{x^8} \end{array}$

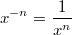
Vorgehen: Festlegung: $x^{-n}=\frac{1}{x^n}$ , Wurzel in Potenzschreibweise, 1., 3. und 4. Potenzgesetz
Bemerkung: Auch hier wurde so umgeformt, dass der Nenner am Ende rational ist (siehe Aufgabe 16).

25)
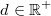
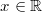
Für alle $d \in \mathbb{R}^+$ und $x\in \mathbb{R}$ gilt:
$\begin{array}{ccl} \sqrt[3]{x^2d} \cdot d^{-\frac{4}{3}} &=& \sqrt[3]{x^2} \cdot \sqrt[3]{d} \cdot d^{-\frac{4}{3}} \\ &=& \sqrt[3]{x^2} \cdot d^\frac{1}{3} \cdot d^{-\frac{4}{3}} \\ &=& \sqrt[3]{x^2} \cdot d^{\frac{1}{3}-\frac{4}{3}} \\ &=& \sqrt[3]{x^2} \cdot d^{-1} \\ &=& \frac{\sqrt[3]{x^2}}{d} \end{array}$

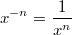
Vorgehen: 4. Potenzgesetz, Wurzel in Potenzschreibweise, 1. Potenzgesetz, Festlegung: $x^{-n}=\frac{1}{x^n}$

26)
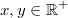
Für alle $x,y \in \mathbb{R}^+$ gilt:
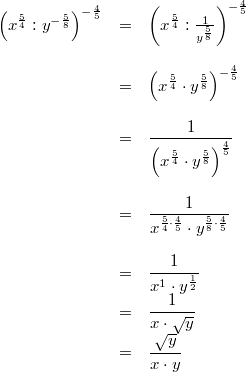$\begin{array}{ccl} \left(x^\frac{5}{4} : y^{-\frac{5}{8}}\right)^{-\frac{4}{5}} &=& \left(x^\frac{5}{4} : \frac{1}{y^\frac{5}{8}}\right)^{-\frac{4}{5}} \\ \\ &=& \left(x^\frac{5}{4} \cdot y^\frac{5}{8}\right)^{-\frac{4}{5}} \\ \\ &=& \dfrac{1}{\left(x^\frac{5}{4} \cdot y^\frac{5}{8}\right)^\frac{4}{5}} \\ \\ &=& \dfrac{1}{x^{\frac{5}{4} \cdot \frac{4}{5}} \cdot y^{\frac{5}{8} \cdot \frac{4}{5}}} \\ \\ &=& \dfrac{1}{x^1 \cdot y^\frac{1}{2}} \\ &=& \dfrac{1}{x\cdot \sqrt{y}} \\ &=& \dfrac{\sqrt{y}}{x\cdot y} \end{array}$

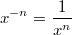
Vorgehen: Festlegung: $x^{-n}=\frac{1}{x^n}$ , mit dem Kehrwert des 2. Bruches multiplizieren, 3. und 4. Potenzgesetz, Potenz in Wurzelschreibweise umformen
Bemerkung: Auch hier wurde so umgeformt, dass der Nenner am Ende rational ist (siehe Aufgabe 16).

27)
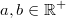
Für alle $a, b\in \mathbb{R}^+$ gilt:
$\begin{array}{ccl} \sqrt[5]{\dfrac{\sqrt[4]{\left(a^4b^2\right)^{10}}}{\sqrt{a^{10}b^5}}} &=& \sqrt[5]{\dfrac{\sqrt[4]{a^{40}b^{20}}}{\sqrt{a^{10}b^5}}} \\ \\ &=& \sqrt[5]{\dfrac{a^{40\cdot \frac{1}{4}}b^{20 \cdot \frac{1}{4}}}{a^{10 \cdot \frac{1}{2}}b^{5 \cdot \frac{1}{2}}}} \\ \\ &=& \sqrt[5]{\dfrac{a^{10}b^5}{a^5b^\frac{5}{2}}} \\ \\ &=& \dfrac{a^{10 \cdot \frac{1}{5}}b^{5 \cdot \frac{1}{5}}}{a^{5 \cdot \frac{1}{5}}b^{\frac{5}{2} \cdot \frac{1}{5}}} \\ \\ &=& \dfrac{a^2b}{ab^\frac{1}{2}} \\ \\ &=& a^2ba^{-1}b^{-\frac{1}{2}} \\ &=& a^{2-1}b^{1-\frac{1}{2}} \\ &=& ab^\frac{1}{2} \\ &=& a\sqrt{b} \end{array}$

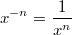
Vorgehen: 3. Potenzgesetz, Wurzeln in Potenzschreibweise, Festlegung: $x^{-n}=\frac{1}{x^n}$ , 1. Potenzgesetz

28)
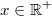
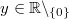
Für alle $x \in \mathbb{R}^+$ und $y \in \mathbb{R}\backslash_{\{0\}}$ gilt:
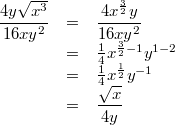$\begin{array}{ccl} \dfrac{4y \sqrt{x^3}}{16xy^2} &=& \dfrac{4x^{\frac{3}{2}}y}{16xy^2} \\ &=& \frac{1}{4} x^{\frac{3}{2}-1}y^{1-2} \\ &=& \frac{1}{4} x^{\frac{1}{2}}y^{-1} \\ &=& \dfrac{\sqrt{x}}{4y} \end{array}$

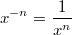
Vorgehen: Wurzel in Potenzschreibweise umformen, Festlegung: $x^{-n}=\frac{1}{x^n}$ , 1. und 2. Potenzgesetz

29)
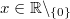
Für alle $x \in \mathbb{R}\backslash_{\{0\}}$ gilt:
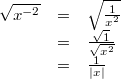$\begin{array}{ccl} \sqrt{x^{-2}} &=& \sqrt{\frac{1}{x^2}} \\ &=& \frac{\sqrt{1}}{\sqrt{x^2}} \\ &=& \frac{1}{\vert x \vert} \end{array}$

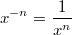
Vorgehen: Festlegung: $x^{-n}=\frac{1}{x^n}$ , 4. Potenzgesetz
Bemerkung 1: Ein negativer Exponent erzeugt einen Bruch. Das Ergebnis muss nicht zwangsläufig auch negativ sein. Im Gegenteil: Ist der Exponent eine gerade Zahl, kann das Ergebnis nie negativ werden. Deshalb kann hier problemlos die Wurzel gezogen werden.
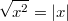
Bemerkung 2: Bitte beachten Sie, dass $\sqrt{x^2} = \vert x \vert$

30)
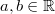
Für alle $a,b \in \mathbb{R}$ gilt:
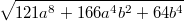$\sqrt{121a^8+166a^4b^2+64b^4}$

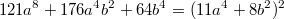
Bemerkung: Der Term unter der Wurzel lässt sich nicht in ein Produkt umformen, da der mittlere Term nicht dem entspricht, was für die Anwendung der 1. Binomischen Formel nötig wäre (siehe Aufgabe 13). Stünde unter der Wurzel 121a^8+176a^4b^2+64b^4= (11a^4+8b^2)^2

, dann könnte man die 1. Binomische Formel anwenden. Da das hier nicht der Fall ist und aus Summen keine Wurzeln gezogen werden können, kann man nicht weiter vereinfachen.

31)
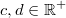
Für alle $c,d \in \mathbb{R}^+$ gilt:
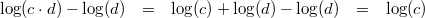$\begin{array}{rcccl} \log(c \cdot d)-\log(d) &=& \log(c) + \log(d) - \log(d) &=& \log(c) \end{array}$

Vorgehen: 1. Logarithmengesetz

32)
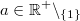
Für alle $a\in\mathbb{R}^+\backslash_{\{1\}}$ gilt:
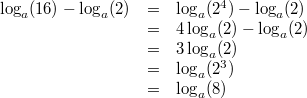$\begin{array}{ccl} \log_a(16)-\log_a(2) &=& \log_a(2^4)-\log_a(2) \\ &=& 4\log_a(2)-\log_a(2) \\ &=& 3\log_a(2) \\ &=& \log_a(2^3) \\ &=& \log_a(8) \end{array}$

Vorgehen: 3. Logarithmengesetz

33)
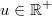
Für alle $u\in \mathbb{R}^+$ gilt:
$\begin{array}{ccl} \frac{\ln\left(u^5\right)}{5} &=& \frac{1}{5}\ln\left(u^5\right) \\ &=& \ln \left(\left(u^5\right)^\frac{1}{5}\right) \\ &=& \ln\left(\sqrt[5]{u^5}\right) \\ &=& \ln(u) \end{array}$

Vorgehen: 3. Logarithmengesetz, 3. Potenzgesetz, Potenz- in Wurzelschreibweise umformen

34)
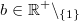
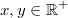
Für alle $b\in\mathbb{R}^+\backslash_{\{1\}}$ und $x,y \in \mathbb{R}^+$ gilt:
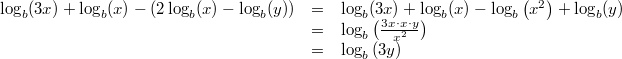$\begin{array}{ccl} \log_b(3x)+\log_b(x)-(2\log_b(x)-\log_b(y)) &=& \log_b(3x)+\log_b(x)-\log_b\left(x^2\right)+\log_b(y) \\ &=& \log_b\left(\frac{3x \cdot x \cdot y}{x^2}\right) \\ &=& \log_b\left(3y\right) \end{array}$

Vorgehen: 2. und 3. Logarithmengesetz
Bemerkung: Achten Sie auf das Minuszeichen vor der Klammer!

35)
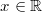
Für alle $x\in \mathbb{R}$ gilt:
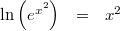$\begin{array}{rcl}\ln\left(e^{x^2}\right) &=& x^2 \end{array}$

Vorgehen: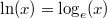 $\ln(x)=\log_e(x)$ und e^x

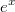
sind Gegenoperationen. Sie heben sich in ihrer Wirkung also auf.

36)
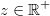
Für alle $z\in \mathbb{R}^+$ gilt:
$\begin{array}{rcccl} 3\log\left(\sqrt[3]{z}\right) &=& \log\left(\left(\sqrt[3]{z}\right)^3\right) &=& \log(z) \end{array}$

Vorgehen: 3. Logarithmengesetz, 3. Potenzgesetz

37)
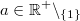
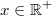
Für alle $a\in\mathbb{R}^+\backslash_{\{1\}}$ und $x\in \mathbb{R}^+$ gilt:
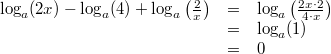$\begin{array}{ccl} \log_a(2x)-\log_a(4)+\log_a\left(\frac{2}{x}\right) &=& \log_a\left(\frac{2x\cdot 2}{4 \cdot x}\right) \\ &=& \log_a(1) \\ &=& 0 \end{array}$

Vorgehen: 1. und 2. Logarithmengesetz

38)
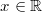
Für alle $x\in \mathbb{R}$ gilt:
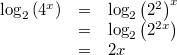$\begin{array}{ccl} \log_2\left(4^x\right) &=& \log_2\left(2^2\right)^x \\ &=& \log_2\left(2^{2x}\right) \\ &=& 2x \end{array}$

Vorgehen: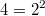 4=2^2

, 3. Potenzgesetz, der Logarithmus zur Basis

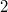
ist die Gegenoperation zu 2^x

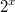
39)
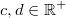
Für alle $c,d\in \mathbb{R}^+$ mit d<c

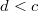
gilt:
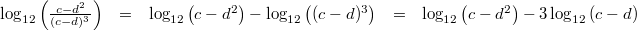$\begin{array}{rcccl} \log_{12}\left(\frac{c-d^2}{(c-d)^3}\right) &=& \log_{12}\left(c-d^2\right)-\log_{12}\left((c-d)^3\right) &=& \log_{12}\left(c-d^2\right)-3\log_{12}\left(c-d\right) \end{array}$

Vorgehen: 2. und 3. Logarithmengesetz
Bemerkung: Es gibt kein Gesetz für die Vereinfachung vom Logarithmus einer Summe. Deswegen können der Zähler- und den Nennerterm nicht weiter vereinfacht werden.

40)
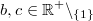
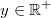
Für alle $b,c\in\mathbb{R}^+\backslash_{\{1\}}$ und $y\in \mathbb{R}^+$ gilt:
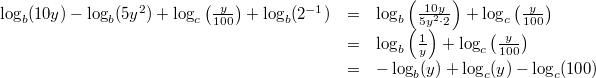$\begin{array}{ccl} \log_b(10y)-\log_b(5y^2)+\log_c\left(\frac{y}{100}\right)+\log_b(2^{-1}) &=& \log_b\left(\frac{10y}{5y^2 \cdot 2}\right)+\log_c\left(\frac{y}{100}\right) \\ &=& \log_b\left(\frac{1}{y}\right)+\log_c\left(\frac{y}{100}\right) \\ &=& -\log_b(y)+\log_c(y)-\log_c(100) \end{array}$

Vorgehen: 1. und 2. Logarithmengesetz
Bemerkung: Achten Sie auf die unterschiedlichen Basen!

41)
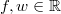
Für alle $f,w \in \mathbb{R}$ mit

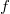
und

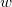
nicht gleichzeitig

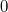
gilt:
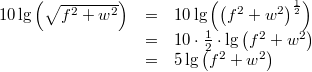$\begin{array}{ccl} 10 \lg \left( \sqrt{f^2+w^2} \right) &=& 10 \lg \left( \left( f^2+w^2 \right)^\frac{1}{2} \right) \\ &=& 10 \cdot \frac{1}{2} \cdot \lg \left( f^2+w^2 \right) \\ &=& 5 \lg \left( f^2+w^2 \right) \end{array}$

Vorgehen: Wurzel in Potenzschreibweise, 3. Logarithmengesetz
Bemerkung 1: Es gibt kein Gesetz für die Vereinfachung vom Logarithmus einer Summe. Deswegen kann der Term nicht weiter vereinfacht werden
Bemerkung 2: "

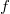
und

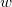
nicht gleichzeitig

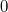
" bedeutet, dass alle Zahlenkombinationen für

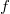
und

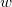
eingesetzt werden dürfen, außer f=w=0

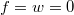
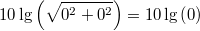
. Dann würde sich nämlich $10 \lg \left( \sqrt{0^2+0^2} \right)=10 \lg \left(0\right)$ ergeben und das ist nicht definiert.

42)
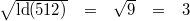$\begin{array}{rcccl} \sqrt{\text{ld}(512)} &=& \sqrt{9} &=& 3 \end{array}$

Vorgehen: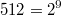 512=2^9

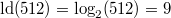
, d. h. $\text{ld}(512)=\log_2(512)=9$

43)
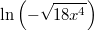$\ln\left(-\sqrt{18x^4}\right)$

Bemerkung: Dieser Term ist nicht definiert, da das Ergebnis einer Wurzel immer positiv oder

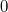
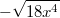
ist. Also ist $-\sqrt{18x^4}$ immer negativ oder

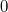
. Der Logarithmus ist aber nur für positive Zahlen definiert.

44)
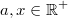
Für alle $a,x \in \mathbb{R}^+$ gilt:
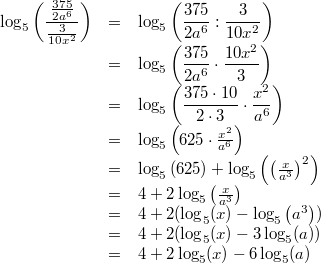$\begin{array}{ccl} \log_5\left(\dfrac{\frac{375}{2a^6}}{\frac{3}{10x^2}}\right) &=& \log_5\left(\dfrac{375}{2a^6} : \dfrac{3}{10x^2}\right) \\ &=& \log_5\left(\dfrac{375}{2a^6} \cdot \dfrac{10x^2}{3}\right) \\ &=& \log_5\left(\dfrac{375 \cdot 10}{2 \cdot 3} \cdot \dfrac{x^2}{a^6}\right) \\ &=& \log_5\left(625 \cdot \frac{x^2}{a^6}\right) \\ &=& \log_5\left(625\right) + \log_5\left( \left(\frac{x}{a^3}\right)^2 \right) \\ &=& 4+2\log_5\left(\frac{x}{a^3}\right) \\ &=& 4+2(\log_5(x)-\log_5\left(a^3\right)) \\ &=& 4+2(\log_5(x)-3\log_5(a)) \\ &=& 4+2\log_5(x)-6\log_5(a) \end{array}$

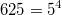
Vorgehen: Doppelbruch auflösen durch Multiplikation mit dem Kehrwert des Nennerbruches, 625=5^4

, 1., 2. und 3. Logarithmengesetz

45)
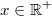
Für alle $x \in \mathbb{R}^+$ gilt:
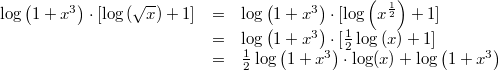$\begin{array}{ccl} \log\left(1+x^3\right) \cdot \lbrack \log\left(\sqrt{x}\right)+1 \rbrack &=& \log\left(1+x^3\right) \cdot \lbrack \log\left(x^\frac{1}{2}\right)+1 \rbrack \\ &=& \log\left(1+x^3\right) \cdot \lbrack \frac{1}{2} \log\left(x\right)+1 \rbrack \\ &=& \frac{1}{2}\log\left(1+x^3\right) \cdot \log(x)+ \log\left(1+x^3\right) \end{array}$

Vorgehen: 3. Logarithmengesetz, ausmultiplizieren
Bemerkung: Es gibt nicht nur kein Logarithmengesetz für die Vereinfachung eines Logarithmusterms, der eine Summe enthält; es gibt ebenfalls kein Gesetz für die Vereinfachung eines Produkts aus mehreren Logarithmustermen. Hier können nur die allgemeinen Rechenregeln angewendet werden.

4. Aufgabe

Den Katzen sind $7 \cdot 7 \cdot 7 \cdot 7 \cdot 7 = 7^5 = 16.807$ Maß Gerste zu verdanken.

Erklärungen

Aufgaben