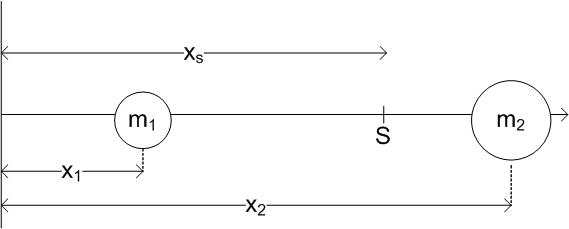
| Abbildung 76: Schwerpunktsbestimmung |
Für einen Körper im Gleichgewicht gilt:
r1 · m1 · g = r2 · m2 · g .

Abbildung 76: Schwerpunktsbestimmung
.
 .
.
.
.
Beispiel 14 - 31
in9026 .
Vier Container mit 15, 30, 45 und 15 Tonnen und jeweils 10 m Länge (Schwerpunkt in der Mitte) sollen entsprechend der Abbildung in ein Flugzeug eingeladen werden. .
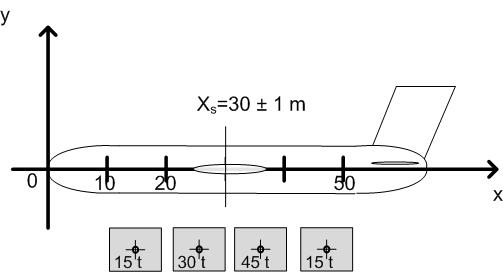
Abbildung 77: Beladung eines Flugzeugs
.
Die Ladezone beginnt 10 m vom Bug entfernt. Der Hersteller schreibt vor, daß der Schwerpunkt 30 m vom Bug entfernt sein muss mit einer Toleranz von 30 ± 1 m. Wird durch die gezeigte Ladereihenfolge diese Vorschrift eingeladen ? .
.
.
Lösung ansehen .
.
.
Die Masse von Flächen mit gleicher Dichte σ bestimmt sich einfach über m=A· σ. Die Flächen können gedanklich in Teilflächen zerlegt werden. Kennt man die Einzelschwerpunkte, so kann man den Gesamtschwerpunkt analog berechnen:
.
Beispiel 14 - 32
in9027 .
Zu bestimmen sei der Schwerpunkt einer Treppe in x- und y-Richtung.
Die Einzelschwerpunkte liegen jeweils mittig. .
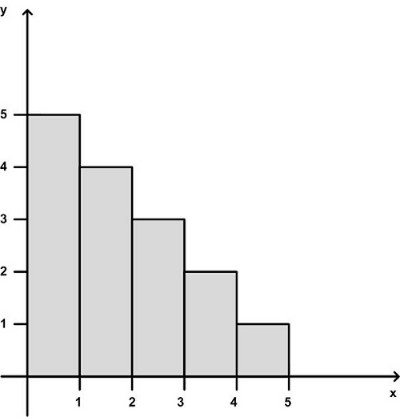
Abbildung 78: Schwerpunkt einer Treppe
.
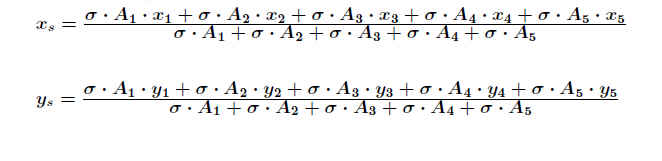 .
.
.
.
Lösung ansehen .
.
.
Hat man ebene Flächen, deren Begrenzung über eine Funktion angegeben ist, macht man einen Übergang von der diskreten Addition zur Integration: .
.
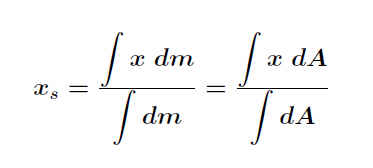 .
.
.
Beispiel 14 - 33 in9023
Gegeben sei ein Dreieck, das durch die x-Achse, y-Achse und die Funktion y=h−h/b · x begrenzt ist: .
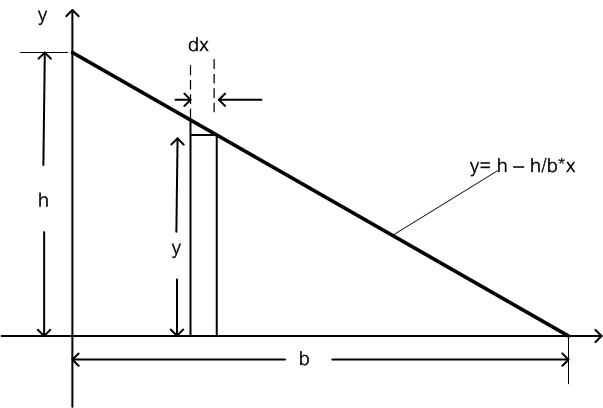
Abbildung 79: Schwerpunkt eines Dreiecks
Zu bestimmen ist zunächst die x-Koordinate des Schwerpunkts: .
 .
.
.
Hierzu zerteilen wir das Dreieck (willkürlich) in lauter senkrechte kleine Stäbchen mit der Fläche
dA = y · dx. .
Hiermit sind die Integralgrenzen vorgegeben zwischen 0 und b. .
.
.
Lösung ansehen .
.
Beispiel 14 - 34 in9024
Alternative Berechnung: Wir zerteilen das Dreieck (willkürlich) in lauter waagrechte kleine Stäbchen mit der Fläche
dA = x · dy. .
Hiermit sind die Integralgrenzen vorgegeben zwischen 0 und h. .
Der Schwerpunkt eines einzelnen Stäbchens liegt bei x = x/2.
Damit erhält man einen Ausdruck für den Schwerpunkt des Dreiecks: .
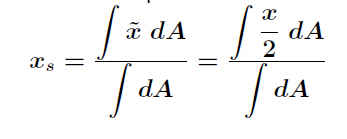 .
.
.
.
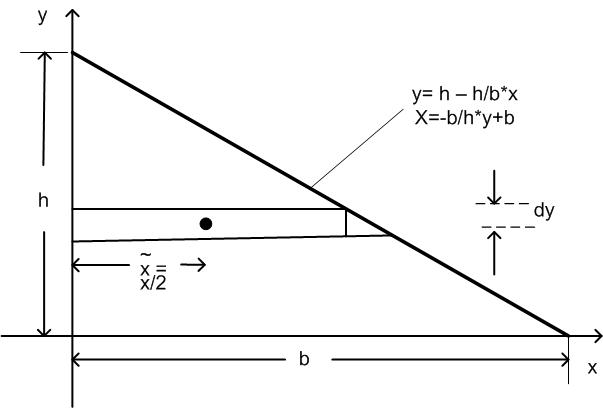
Abbildung 80: Schwerpunkt eines Dreiecks
.
.
Lösung ansehen .
.
Beispiel 14 - 35 in9028
Zu bestimmen sei die x-Koordinate des Schwerpunkts der Fläche, die durch die x-Achse, y-Achse und die Funktion y=1−x2 begrenzt ist.
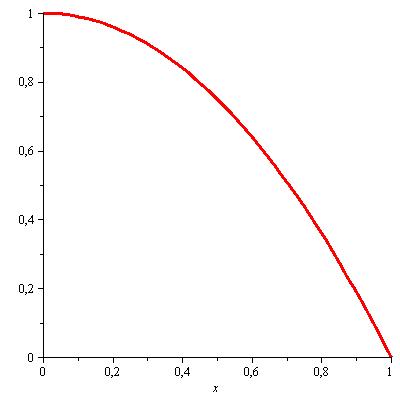
Abbildung 81: Schwerpunkt einer Fläche
.
.
Lösung ansehen .
.
Beispiel 14 - 36 in9025
Berechnung des Schwerpunkts eines Viertelkreises: .
Bleibt man hier in der Darstellung kartesischer Koordinaten, wird die Berechnung wesentlich aufwendiger, wie das Beispiel für die y-Koordinate zeigt: .
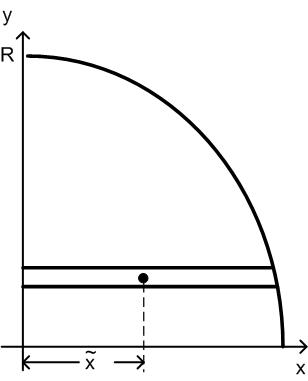
Abbildung 82: Schwerpunkt eines Viertelkreises
.
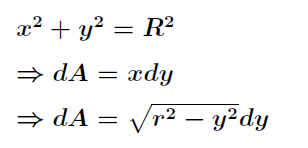 .
.
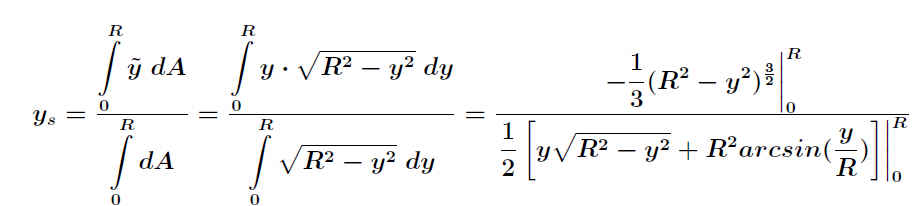 .
.
.
Eine alternative Berechnung geht wie folgt: Wir zerteilen den Kreisbogen (willkürlich) in lauter kleine Kreissegmente
dL = R · dϕ. .
Hier sind die Integralgrenzen einfach angebbar, sie liegen zwischen 0 und π/2. .
Haben wir die Schwerpunkte der einzelnen kreissegmente, können wir den Schwerpunkt des Viertelkreises daraus bestimmen. .
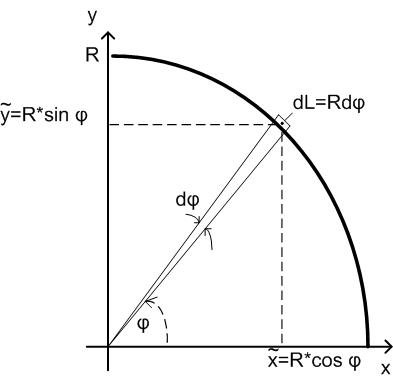
Abbildung 83: Schwerpunkt eines Viertelkreises
.
Der Schwerpunkt eines einzelnen Stückchens liegt bei x = R · cosϕ bzw. ỹ = R · sinϕ .
Damit erhält man einen Ausdruck für den Schwerpunkt eines Viertelkreisbogens: .
.
.
Lösung ansehen .
.
Entsprechend ist der Schwerpunkt eines Halbkreisbogens: .
xs= 2R/ π , und aus Symmetriegründen: ys=0. .
Bildet man nun die Summe eines Viertelkreises aus diesen Viertelkreisbögen, so ist der Schwerpunkt xs=4R/3π.
Weitere Beispiele finden sich in []. .
Ist der Gegenstand nun kein ebenes, sondern ein dreidimensionales Gebilde, muss ein Ausdruck für das jeweilige Massenelement (z.B. Stäbchen) bezüglich x gebildet werden, unter Umständen kann auch hier eine Integration notwendig werden. Dann spricht man von Mehrfachintegralen. .
Analog können auch die Massenträgheitsmomente J = ∫m r2 dm gebildet werden: Für jedes Masseteilchen dm wird das Produkt des Abstandsquadrats zur jeweiligen Drehachse gebildet und damit das bestimmte Integral für alle Massenteilchen bestimmt. Auf mathematischer Seite ändert sich hier nichts. .