ErklärungenFunktionenDefinition: Eine Funktion ist eine Zuordnung, die jedem Element einer Menge, Definitionsbereich (Formelzeichen: 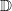 ) genannt, genau ein Element einer anderen Menge, Wertebereich (Formelzeichen: 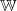 ) genannt, zuordnet. Die Funktionsgleichung wird auch Zuordnungsvorschrift genannt. Das Element des Definitionsbereichs nennt man üblicherweise x-Wert, unabhängige Variable oder Argument der Funktion, das Element des Wertebereichs y-Wert oder abhängige Variable. In diesem Lernmodul werden nur Funktionen betrachtet, deren Definitions- und Wertebereiche aus Teilmengen der reellen Zahlen bestehen und die sich im weitesten Sinne "vernünftig" verhalten. Es gibt Funktionen, bei denen einige der hier besprochenen Eigenschaften so nicht gelten - aber darum können Sie sich, wenn nötig, später kümmern... Berechnung von Funktionswerten: Ist eine Funktion 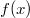 gegeben, dann bedeutet "Funktionswerte berechnen" für die Variable konkrete Zahlenwerte einzusetzen und den so entstehenden Term auszurechnen. Fasst man diese Ergebnisse in einer Tabelle zusammen, üblicherweise geordnet nach der Größe der x-Werte, erhält man eine Wertetabelle. Beispiel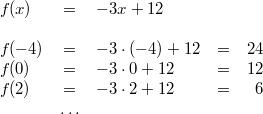 Bemerkung: Bitte beachten Sie die Schreibweise: Die Variable, hier  , wird auf beiden Seiten der Funktionsgleichung durch den Zahlenwert ersetzt. Wertetabelle Bemerkung: Bei der Wahl der x-Werte für die Wertetabelle muss auf die Besonderheiten der Funktion Rücksicht genommen werden. Hätte die Funktion ein Minimum bei  , würden wir das bei dieser Wertetabelle wahrscheinlich nicht bemerken. Häufig sind die ganzen Zahlen von 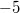 bis 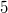 aber schon recht gute Kandidaten. FunktionsgraphenDefinition: Ein Funktionsgraph ist die grafische Darstellung einer Funktion in einem Koordinatensystem. Für eine solche grafische Darstellung zeichnet man zunächst die Punkte aus der Wertetabelle in der Form 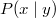 in das Koordinatensystem und verbindet diese anschließend mit einer Linie. Beispiele für Funktionsgraphen Beispiele für Kurven in einem Koordinatensystem, die keine Funktionen darstellenBei allen folgenden Beispielen wird nicht jedem x-Wert eindeutig ein y-Wert zugeordnet. Hier gibt es immer auch x-Werte, zu denen mehrere y-Werte gefunden werden und x-Werte, die keinen y-Wert zugeordnet bekommen. Z. B. findet man im ersten Bild zu 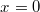 einen positiven und einen negativen y-Wert. Auf der anderen Seite findet man zu 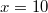 (und zu vielen anderen x-Werten) gar keinen y-Wert. Daher handelt es sich bei den Zuordnungen nicht um Funktionen und bei ihren grafischen Darstellungen nicht um Funktionsgraphen. Lineare FunktionenDer Graph einer linearen Funktion ist eine Gerade. Die allgemeine Geradengleichung, mit der lineare Funktionen beschrieben werden, lautet: 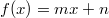 mit 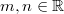 , wobei  die Steigung der Geraden bezeichnet und 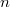 den y-Achsenabschnitt. Das bedeutet: - An
 kann man ablesen, um wie viele Einheiten des y-Wert steigt oder fällt, wenn kann man ablesen, um wie viele Einheiten des y-Wert steigt oder fällt, wenn  um eine Einheit größer wird. um eine Einheit größer wird. -
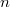 gibt die y-Koordinate des Punktes an, an dem die Gerade die y-Achse des Koordinatensystems schneidet. gibt die y-Koordinate des Punktes an, an dem die Gerade die y-Achse des Koordinatensystems schneidet.
Bemerkung 1: Nicht jede Gerade in einem Koordinatensystem ist Graph einer linearen Funktion. Senkrechte Geraden verletzen die Funktionsdefinition, da bei ihnen zu einem x-Werte unendlich viele y-Werte gefunden werden können (siehe Bild oben). Bemerkung 2: Zwei Punkte reichen aus, um eine Gerade eindeutig zu bestimmen. Anders formuliert: Durch zwei Punkte verläuft genau eine Gerade. WissenswertesIst  negativ negativ, fällt die Gerade. Ist  positiv positiv, steigt die Gerade. Ist 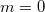 , ist die Gerade konstant. Ist 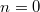 , verläuft die Gerade durch den Koordinatenursprung. Eine solche Gerade nennt man Ursprungsgerade. Beispiele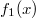 ist eine fallende Ursprungsgerade. 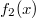 ist eine steigende Gerade. 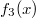 ist eine konstante Gerade. Ermittlung der SteigungSind die Punkte 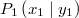 und 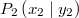 gegeben, lässt sich die Steigung nach folgender Formel berechnen: 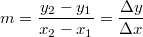 (gesprochen: delta y geteilt durch delta x). Anders formuliert: Die Differenz der y-Werte geteilt durch die Differenz der x-Werte ergibt die Steigung. Falls keine Punkte gegeben sind, liest man aus der Zeichnung zwei Punkte des Graphen ab. Dabei muss beachten werden, dass das Ablesen aus Koordinatensystemen im Gegensatz zum Rechnen keine wirklich genauen Ergebnissen liefert. Zu den Beispielen von obenFür 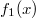 sind die Punkte 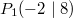 und 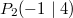 gegeben. Es folgt: | | | | | | | | Für 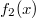 sind die Punkte 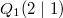 und 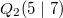 gegeben. Es folgt: | | | | | | | | Für 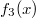 sind die Punkte 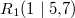 und 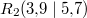 gegeben. Es folgt: | | | | | | | |
Bemerkung 1: Die Vorzeichen der gerade berechneten Steigungswerte stimmen mit den obigen Aussagen überein. Bemerkung 2: Die Steigung kann mithilfe von Steigungsdreiecken veranschaulicht werden (siehe Grafik unten). Man erkennt dabei, dass bei 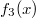 kein Steigungsdreieck eingezeichnet werden kann, denn egal, wie groß man 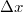 wählt, 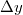 ist immer 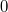 . Daraus ergibt sich auch rechnerisch, dass bei konstanten Geraden die Steigung 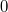 ist, was wohl auch anschaulich deutlich ist. Bemerkung 3: 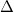 ist der griechische Buchstabe "delta", der in der Mathematik gerne für Differenzen verwendet wird. Die Größe und die Lage des Steigungsdreiecks haben keinen Einfluss auf die Größe der Steigung, da nur das Verhältnis aus den Längen der beiden Dreiecksseiten berechnet wird. Z. B. gilt bei 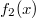 (siehe Grafik unten) Mittleres Steigungsdreieck mit 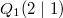 und 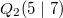 : | | | | | | | | Kleines Steigungsdreieck mit 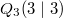 und 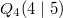 : | | | | | | | | Großes Steigungsdreieck mit 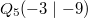 und 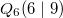 : | | | | | | | |
Ebenfalls keinen Einfluss hat die Reihenfolge, in der man die Punkte in die Steigungsformel einsetzt. Das sieht man z. B. an 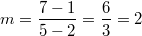 (mittleres Steigungsdreieck). Ermittlung des y-AchsenabschnittsWie der y-Achsenabschnitt 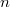 ermittelt werden kann, hängt von der Aufgabenstellung ab: Möchte man die Geradengleichung 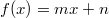 aus zwei gegebenen Punkten ermitteln, benötigt man zunächst die Steigung  . Um den y-Achsenabschnitt zu berechnen, setzt man  und die Koordinaten eines gegebenen Punktes in die Gleichung ein. 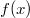 entspricht dabei der y-Koordinate. So erhält man eine lineare Gleichung, die nach 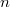 aufgelöst werden kann. Welchen Punkt man für diese Rechnung verwendet, ist egal, da die Gerade ja ohnehin durch beide Punkte verlaufen soll. Der zweite Punkt kann zur Überprüfung des Ergebnisses genutzt werden, indem man seine Koordinaten in die ermittelte Geradengleichung einsetzt und überprüft, ob beide Seiten gleich groß werden ( Punktprobe). Bei den Beispielen berechnet man also Für 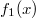 : | | | | daraus folgt | | | | also ist | | | | Für 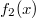 : | | | | daraus folgt | | | | also ist | | | | Für 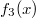 : | | | | daraus folgt | | | | also ist | | | |
Punktproben Für 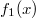 : | | | | daraus folgt | | | | | Das ist eine wahre Aussage. Die berechnete Geradengleichung für 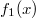 ist also richtig. | Für 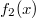 : | | | | daraus folgt | | | | | Das ist eine wahre Aussage. Die berechnete Geradengleichung für 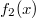 ist also richtig. | Für 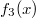 : | | | | daraus folgt | | | | | Das ist eine wahre Aussage. Die berechnete Geradengleichung für 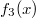 ist also richtig. |
Diese Ergebnisse finden Sie auch in den obigen Zeichnungen wieder. Ist ein Graph gegeben, stellt man einfach fest, wo der Graph die y-Achse schneidet. Der y-Wert dieses Punktes ist der y-Achsenabschnitt. Bemerkung: Wie oben schon gesagt, ist Ablesen kein mathematisch-exaktes Verfahren. Bei 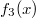 erkennt man gut, welche Schwierigkeiten das Ablesen von Werten aus einer Grafik bereiten kann. Eine präzisere Aussage als "ein Wert zwischen 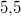 und 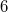 " ist eigentlich nicht möglich. Damit sind die Geradengleichungen vollständig bestimmt. Sie lauten: 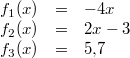 Schnittpunkt zweier GeradenZwei Geraden können Schnittpunkte haben. Z. B. schneiden sich die Funktionen 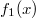 und 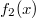 im Punkt 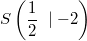 (siehe Grafik oben). Berechnung: Da ein Schnittpunkt ein gemeinsamer Punkt der beiden Geraden ist, müssen die zu diesem x-Wert gehörenden y-Werte der beiden Funktionen übereinstimmen. Man setzt also die beiden Funktionsterme gleich und berechnet daraus, für welche x-Werte die entstehende lineare Gleichung erfüllt ist. BeispielIm Fall von 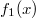 und 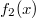 habe der Schnittpunkt die Koordinaten 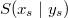 x-Wert berechnen: 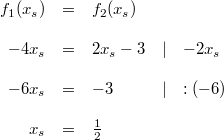 y-Wert berechnen: 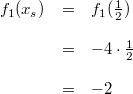 ODER 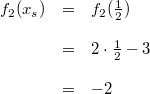 Der Punkt 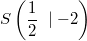 liegt tatsächlich auf beiden Geraden und ist somit der (einzige) Schnittpunkt von 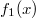 und 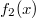 |
|
 Brückenkurs
Brückenkurs