Brotkrumen-Navigation

Brückenkurs » 7 Lineare Gleichungssysteme

  Brückenkurs

zurückErklärungen 
  Aufgabenweiter

Lösungen

1. Aufgabe

1) Lösung nach dem Additionsverfahren
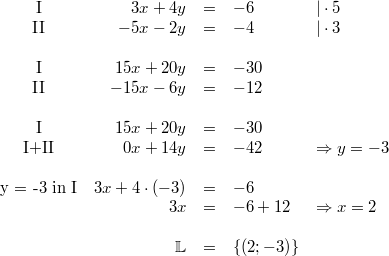
\begin{array}{crclllcc} \mbox{I} & 3x+4y &=& -6 & \vert \cdot 5 \\ \mbox{II} & -5x-2y &=& -4 & \vert \cdot 3 \\ \\ \mbox{I} & 15x+20y &=& -30 \\ \mbox{II} & -15x-6y &=& -12 \\ \\ \mbox{I} & 15x+20y &=& -30 \\ \mbox{I+II} & 0x +14y &=& -42 & \Rightarrow y = -3 \\ \\ \mbox{y = -3 in I} & 3x+4 \cdot (-3) &=& -6 \\ & 3x &=& -6+12 & \Rightarrow x = 2 \\ \\ & \mathbb{L} &=& \{\left(2; -3\right)\} \end{array}


2) Lösung nach dem Additionsverfahren
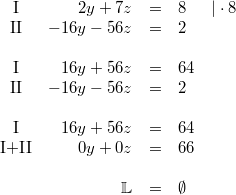\begin{array}{crclllcc} \mbox{I} & 2y+7z &=& 8 & \vert \cdot 8 \\ \mbox{II} & -16y-56z &=& 2 \\ \\ \mbox{I} & 16y+56z &=& 64 \\ \mbox{II} & -16y-56z &=& 2 \\ \\ \mbox{I} & 16y+56z &=& 64 \\ \mbox{I+II} & 0y+0z &=& 66 \\ \\ & \mathbb{L} &=& \emptyset \end{array}

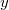
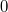
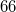
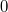
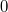
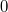
Bemerkung: Es gibt keine Zahlen y und z, die jeweils mit 0 multipliziert und dann addiert, 66 ergeben. Das Produkt aus einer beliebigen reellen Zahl und 0 ist immer 0, die Summe von 0 und 0 ebenfalls. Daher ist diese Gleichung nicht lösbar.


3) Lösung nach dem Additionsverfahren
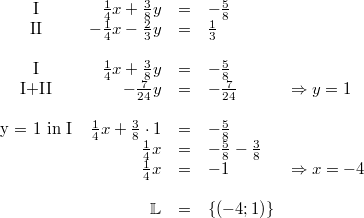
\begin{array}{crclllcc} \mbox{I} & \frac{1}{4}x+\frac{3}{8}y &=& -\frac{5}{8} \\ \mbox{II} & -\frac{1}{4}x-\frac{2}{3}y &=& \frac{1}{3} \\ \\ \mbox{I} & \frac{1}{4}x+\frac{3}{8}y &=& -\frac{5}{8} \\ \mbox{I+II} & -\frac{7}{24}y &=& -\frac{7}{24} & \Rightarrow y = 1 \\ \\ \mbox{y = 1 in I} & \frac{1}{4}x+\frac{3}{8} \cdot 1 &=& -\frac{5}{8} \\ & \frac{1}{4}x &=& -\frac{5}{8}-\frac{3}{8} \\ & \frac{1}{4}x &=& -1 & \Rightarrow x = -4 \\ \\ & \mathbb{L} &=& \{\left(-4; 1\right)\} \end{array}


4) Lösung nach dem Einsetzungsverfahren
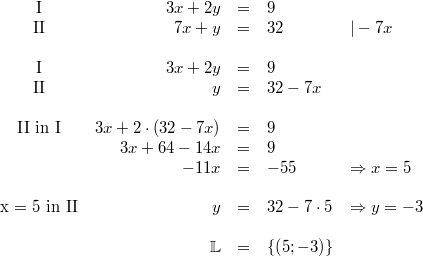
\begin{array}{crclllcc} \mbox{I} & 3x+2y &=& 9 \\ \mbox{II} & 7x+y &=& 32 & \vert -7x \\ \\ \mbox{I} & 3x+2y &=& 9 \\ \mbox{II} & y &=& 32-7x \\ \\ \mbox{II in I} & 3x+2 \cdot (32-7x) &=& 9 \\ & 3x+64-14x &=& 9 \\ & -11x &=& -55 & \Rightarrow x = 5 \\ \\ \mbox{x = 5 in II} & y &=& 32-7 \cdot 5 & \Rightarrow y = -3 \\ \\ & \mathbb{L} &=& \{\left(5; -3 \right) \} \end{array}


5) Lösung nach dem Gleichsetzungsverfahren
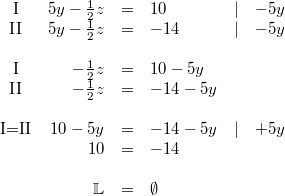\begin{array}{crclllcc} \mbox{I} & 5y-\frac{1}{2}z &=& 10 &\vert& -5y \\ \mbox{II} & 5y-\frac{1}{2}z &=& -14 &\vert& -5y \\ \\ \mbox{I} & -\frac{1}{2}z &=& 10-5y \\ \mbox{II} & -\frac{1}{2}z &=& -14-5y \\ \\ \mbox{I=II} & 10-5y &=& -14-5y &\vert& +5y \\ & 10 &=& -14 \\ \\ & \mathbb{L} &=& \emptyset \end{array}

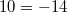
Bemerkung: 10=-14 ist ein Widerspruch. Daher ist dieses Gleichungssystem nicht lösbar. Das hätte man allerdings auch ohne Rechnung erkennen können, da auf den linken Seiten der beiden Gleichungen jeweils der gleiche Term stand, aber unterschiedliche Ergebnisse vorgegeben waren. Für solche Gleichungssysteme kann es keine Lösung geben.


6) Lösung nach dem Gleichsetzungsverfahren
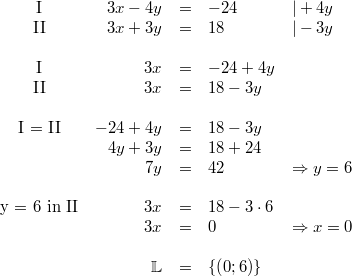
\begin{array}{crclllcc} \mbox{I} & 3x-4y &=& -24 & \vert +4y \\ \mbox{II} & 3x+3y &=& 18 & \vert -3y \\ \\ \mbox{I} & 3x &=& -24+4y \\ \mbox{II} & 3x &=& 18-3y \\ \\ \mbox{I = II} & -24+4y &=& 18-3y \\ & 4y+3y &=& 18+24 \\ & 7y &=& 42 & \Rightarrow y = 6 \\ \\ \mbox{y = 6 in II} & 3x &=& 18-3 \cdot 6 \\ & 3x &=& 0 & \Rightarrow x = 0 \\ \\ & \mathbb{L} &=& \{\left(0; 6\right)\} \end{array}


7) Lösung nach dem Additionsverfahren
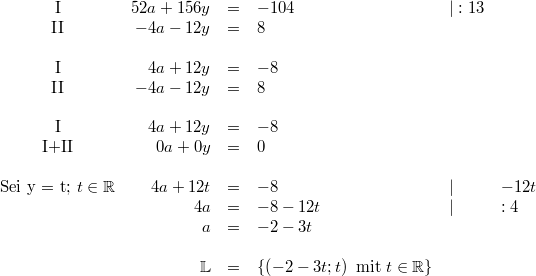\begin{array}{crclllcc} \mbox{I} & 52a+156y &=& -104 & \vert : 13 \\ \mbox{II} & -4a-12y &=& 8 \\ \\ \mbox{I} & 4a+12y &=& -8 \\ \mbox{II} & -4a-12y &=& 8 \\ \\ \mbox{I} & 4a+12y &=& -8 \\ \mbox{I+II} & 0a+0y &=& 0 \\ \\ \mbox{Sei y = t; }t \in \mathbb{R} & 4a+12t &=& -8 & \vert & -12t \\ & 4a &=& -8-12t & \vert & :4 \\ & a &=& -2-3t \\ \\ & \mathbb{L} &=& \{\left(-2-3t; t\right) \mbox{ mit }t \in \mathbb{R}\} \end{array}

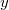
Bemerkung: Gleichung I+II ergibt für alle reellen Zahlen a und y eine wahre Aussage. Die Lösung dieses linearen Gleichungssystems hängt also alleine von Gleichung I ab. Da eine lineare Gleichung mit zwei Variablen vorliegt, muss eine Variable festgelegt werden. Wir wählen hier y=t; t \in \mathbb{R}. t ist dabei ein so genannter Parameter. Anschließend kann man für a nicht mehr eine beliebige Zahl einsetzen, wenn Gleichung I erfüllt sein soll. 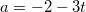Die Gleichung führt nur dann zu einer wahren Aussage, wenn a=-2-3t ist. Man findet also unendlich viele Zahlenpaare, die dieses lineare Gleichungssystem erfüllen, z. B.
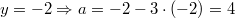y=-2 \Rightarrow a = -2-3 \cdot (-2) = 4
Probe: \begin{matrix} \mbox{I} & 52 \cdot 4+156 \cdot (-2) &=& 208-312 &=& -104 \\ \mbox{II} & -4 \cdot 4-12 \cdot (-2) &=& -16+24 &=& 8 \end{matrix}
Beide Gleichungen ergeben also wahre Aussagen.

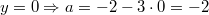y=0 \Rightarrow a = -2-3 \cdot 0 = -2
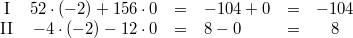
Probe: \begin{array}{crclcc} \mbox{I} & 52 \cdot (-2)+156 \cdot 0 &=& -104+0 &=& -104 \\ \mbox{II} & -4 \cdot (-2)-12 \cdot 0 &=& 8-0 &=& 8 \end{array}
Beide Gleichungen ergeben also wahre Aussagen.

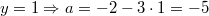y=1 \Rightarrow a = -2-3 \cdot 1 = -5
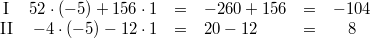
Probe: \begin{array}{crclcc} \mbox{I} & 52 \cdot (-5)+156 \cdot 1 &=& -260+156 &=& -104 \\ \mbox{II} & -4 \cdot (-5)-12 \cdot 1 &=& 20-12 &=& 8 \end{array}
Beide Gleichungen ergeben also wahre Aussagen.

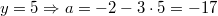y=5 \Rightarrow a = -2-3 \cdot 5 = -17
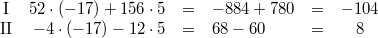
Probe: \begin{array}{crclcc} \mbox{I} & 52 \cdot (-17)+156 \cdot 5 &=& -884+780 &=& -104 \\ \mbox{II} & -4 \cdot (-17)-12 \cdot 5 &=& 68-60 &=& 8 \end{array}
Beide Gleichungen ergeben also wahre Aussagen.


8) Lösung nach dem Additionsverfahren
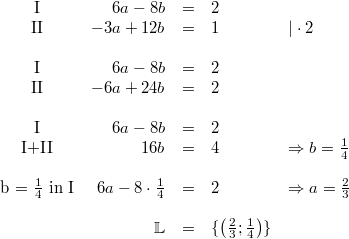
\begin{array}{crclllcc} \mbox{I} & 6a-8b &=& 2 \\ \mbox{II} & -3a+12b &=& 1 & \vert \cdot 2 \\ \\ \mbox{I} & 6a-8b &=& 2 \\ \mbox{II} & -6a+24b &=& 2 \\ \\ \mbox{I} & 6a-8b &=& 2 \\ \mbox{I+II} & 16b &=& 4 & \Rightarrow b = \frac{1}{4} \\ \\ \mbox{b = } \frac{1}{4} \mbox{ in I} & 6a-8 \cdot \frac{1}{4} &=& 2 & \Rightarrow a = \frac{2}{3} \\ \\ & \mathbb{L} &=& \{\left(\frac{2}{3}; \frac{1}{4}\right)\} \end{array}

2. Aufgabe

Sei h die Anzahl der Hühner und s die Anzahl der Schweine (siehe Bemerkung zu Textaufgaben).

Dann gilt:
I h+s=37
Denn jedes der Tiere hat genau einen Kopf.
II 2h+4s=90
Denn jedes Huhn hat 2 Beine, also haben h Hühner zusammen 2h Beine. Schweine haben 4 Beine, also haben s Schweine 4s Beine. Zusammen haben alle Tiere folglich 2h+4s Beine.

Rechnerische Lösung (Additionsverfahren):
Zu lösen ist also das folgende lineare Gleichungssystem:
\begin{array}{crclllcc} \mbox{I} & h+s &=& 37 & \vert \cdot (-2) \\ \mbox{II} & 2h+4s &=& 90 \\ \\ \mbox{I} & -2h-2s &=& -74 \\ \mbox{II} & 2h+4s &=& 90 \\ \\ \mbox{I} & -2h-2s &=& -74 \\ \mbox{I+II} & 2s &=& 16 & \Rightarrow s = 8 \\ \\ \mbox{s = 8 in I} & h+8 &=& 37 & \Rightarrow h = 29 \end{array}

Herr Müller hat 29 Hühner und 8 Schweine.


Zeichnerische Lösung:
Man formt die Gleichungen I und II von oben so um, dass sie der allgemeinen Geradengleichung entsprechen, nämlich:
I h+s=37 \Rightarrow f_1(h)=s=37-h

II 2h+4s=90 \Rightarrow f_2(h)=s=\frac{45}{2}-\frac{1}{2}h

Diese beiden Geraden können dann in ein Koordinatensystem eingetragen und der Schnittpunkt abgelesen werden.
die entsprechenden zwei Geraden im Koordinatensystem
Der Schnittpunkt der beiden Geraden liegt bei S(29 \mid 8) . h, also die Anzahl der Hühner, ist 29 und s, also die Anzahl der Schweine, ist 8. Jedes andere Ergebnis hätte uns stutzig machen sollen...

Da in diesem Zusammenhang offensichtlicherweise nur ganzzahlige Lösungen sinnvoll sind, ist die folgende Grafik, in der keine Geraden, sondern einzelne Punkte an den entsprechenden Stellen eingezeichnet wurden, besser:
2 Gerade im Koordinatensystem mit Punkte gezeichnet

3. Aufgabe

Sei b die Anzahl der billigen Schokoladentäfelchen und t die Anzahl der teuren Schokoladentäfelchen (siehe Bemerkung zu Textaufgaben).
Eine billige Schokolade kostet laut Aufgabenstellung 0{,}06 EUR, eine teure 0{,}14 EUR.

a)
Es gilt: 0{,}06b + 0{,}14t = 11{,}20
Der Preis für eine billigen Schokolade mal die Anzahl der billigen Schokoladentafeln plus den Preis für eine teure Schokolade mal die Anzahl der teuren Tafeln ergibt den Gesamtpreis.

Mögliche Ergebnisse (b; t) sind also: (0; 80), (7; 77), (14; 74), (21; 71),…, (161; 11), (168; 8), (175; 5), (182; 2)
Denn 0{,}06 \cdot 0+0{,}14 \cdot 80 = 11{,}20 usw.

Bitte achten Sie darauf, dass hier nur ganzzahlige Angaben infrage kommen!


b)
Zur oberen Gleichung kommt dazu: b+t = 100
Denn die Gesamtzahl der Schokoladentäfelchen soll 100 betragen.

Es ergibt sich das folgende lineare Gleichungssystem, das mit dem Einsetzungsverfahren gelöst wird:
\begin{array}{crclcl} \mbox{I} & 0{,}06b+0{,}14t &=& 11{,}20 \\ \mbox{II} & b+t &=& 100 &\vert& -t \\ \\ \mbox{I} & 0{,}06b+0{,}14t &=& 11{,}20 \\ \mbox{II} & b &=& 100-t \\ \\ \mbox{II in I} & 0{,}06 \cdot (100-t)+0{,}14t &=&11{,}20 \\ & 6-0{,}06t+0{,}14t &=& 11{,}20 &\vert& -6 \\ & 0{,}08t &=& 5{,}20 &\vert& : 0{,}08 \\ & t &=& 65 \end{array}

Es sind 65 teure Schokoladen in der Großpackung enthalten.

Bemerkung: Da nur nach der Anzahl der teuren Schokoladentäfelchen gefragt war, kann die Bearbeitung der Aufgabe hier abgebrochen werden. Hätte das Gleichungssystem vollständig gelöst werden sollen, müsste auch für b ein Wert ermittelt werden.

4. Aufgabe

1)
\begin{array}{crcrcrcrl} \mbox{I} & 8x &+& 9y &-& 5z &=& -9 \\ \mbox{II} & -6x &-& 3y &+& 5z &=& -27 \\ \mbox{III} & \frac{1}{2}x &+& y &-& 2z &=& -10 \\ \\ \mbox{I} & 8x &+& 9y &-& 5z &=& -9 \\ \mbox{3 I+4 II} & & & 15y &+& 5z &=& -135 \\ \mbox{I-16 III} & & & -7y &+& 27z &=& 151 \\ \\ \mbox{I} & 8x &+& 9y &-& 5z &=& -9 \\ \mbox{II'} & & & 15y &+& 5z &=& -135 \\ \mbox{7 II'+15 III'} & & & & & 440z &=& 1320 & \Rightarrow z = 3 \\ \\ \mbox{z = 3 in II'} & & & 15y &+& 5 \cdot 3 &=& -135 & \Rightarrow y = -10 \\ \mbox{z = 3 und y = -10 in I} & 8x &+& 9 \cdot \left(-10\right) &-& 5 \cdot 3 &=& -9 & \Rightarrow x = 12 \end{array}

Die Lösungsmenge lautet also \mathbb{L} &=& \{\left(12; -10; 3\right)\}


2)
\begin{array}{crcrcrcrl} \mbox{I} & 7x &+& 5y &-& 10z &=& 12 \\ \mbox{II} & -28x &-& 35y &+& 16z &=& -23 \\ \mbox{III} & -21x &-& 30y &+& 6z &=& 9 \\ \\ \mbox{I} & 7x &+& 5y &-& 10z &=& 12 \\ \mbox{4 I+II} & & & -15y &-& 24z &=& 25 \\ \mbox{3I+III} & & & -15y &-& 24z &=& 45 \\ \\ \mbox{I} & 7x &+& 5y &-& 10z &=& 12 \\ \mbox{II'} & & & -15y &-& 24z &=& 25 \\ \mbox{II'-III'} & & & & & 0 &=& -20 \end{array}

Die Lösungsmenge lautet also \mathbb{L} &=& \emptyset


3)
\begin{array}{crcrcrcrl} \mbox{I} & -\frac{3}{2}a &+& \frac{1}{7}b &+& c &=& 6 \\ \\ \mbox{II} & \frac{5}{6}a &+& \frac{1}{3}b &-& \frac{1}{3}c &=& 2 \\ \\ \mbox{III} & & & -\frac{4}{3}b &-& \frac{5}{3}c &=& -3 \\ \\ \\ \mbox{14 I} & -21a &+& 2b &+& 14c &=& 84 \\ \mbox{6 II} & 5a &+& 2b &-& 2c &=& 12 \\ \mbox{3 III} & & & -4b &-& 5c &=& -9 \\ \\ \mbox{I} & -21a &+& 2b &+& 14c &=& 84 \\ \mbox{5 I+21 II} & & & 52b &+& 28c &=& 672 \\ \mbox{III} & & & -4b &-& 5c &=& -9 \\ \\ \mbox{I} & -21a &+& 2b &+& 14c &=& 84 \\ \mbox{II'} & & & 52b &+& 28c &=& 672 \\ \mbox{II'+13 III'} & & & & & -37c &=& 555 & \Rightarrow c = -15 \\ \\ \mbox{c = -15 in II'} & & & 52b &+& 28 \cdot \left(-15\right) &=& 672 & \Rightarrow b = 21 \\ \mbox{c = -15 und b = 21 in I} & -21a &+& 2 \cdot 21 &+& 14 \cdot \left(-15\right) &=& 84 & \Rightarrow a = -12 \end{array}

Die Lösungsmenge lautet also \mathbb{L} &=& \{\left(-12; 21; -15\right)\}

Bemerkung: Die ersten Umformungen (Multiplikation jeweils mit dem Hauptnenner) wurden durchgeführt, damit in der Folgerechnung keine Brüche mehr auftauchen. Allerdings werden dadurch die Zahlenwerte natürlich größer...


4)
\begin{array}{crcrcrcrl} \mbox{I} & -18x &-& 4y &-& 26z &=& 4 \\ \mbox{II} & 9x &+& 8y &+& 13z &=& -5 \\ \mbox{III} & 9x &-& 12y &+& 7z &=& 11 \\ \\ \mbox{I} & -18x &-& 4y &-& 26z &=& 4 \\ \mbox{I+2 II} & & & 12y & & &=& -6 & \Rightarrow y = -\frac{1}{2} \\ \mbox{I+2 III} & & & -28y &-& 12z &=& 26 \\ \\ \mbox{y = -0,5 in III'} & & & -28\cdot \left(-\frac{1}{2}\right) &-& 12z &=& 26 & \Rightarrow z = -1 \\ \mbox{y = -0,5 und z = -1 in I} & -18x &-& 4 \cdot \left(-\frac{1}{2}\right) &-& 26 \cdot \left(-1\right) &=& 4 & \Rightarrow x = \frac{4}{3} \end{array}

Die Lösungsmenge lautet also \mathbb{L} &=& \left\{\left(\frac{4}{3}; -\frac{1}{2}; -1\right)\right\}


5)
\begin{array}{crcrcrcrl} & 11a &-& 8b &+& c &=& 37 \\ & -a &-& 2b &+& 7c &=& -35 \\ & 12a &+& 9b &-& 6c &=& 12 \\ \\ \mbox{I} & -a &-& 2b &+& 7c &=& -35 \\ \mbox{II} & 11a &-& 8b &+& c &=& 37 \\ \mbox{III} & 12a &+& 9b &-& 6c &=& 12 \\ \\ \mbox{I} & -a &-& 2b &+& 7c &=& -35 \\ \mbox{11 I+II} & & & -30b &+& 78c &=& -348 \\ \mbox{12 I+III} & & & -15b &+& 78c &=& -408 \\ \\ \mbox{I} & -a &-& 2b &+& 7c &=& -35 \\ \mbox{II'} & & & -30b &+& 78c &=& -348\\ \mbox{II'-2 III'} & & & & & -78c &=& 468 & \Rightarrow c = -6 \\ \\ \mbox{c = -6 in II'} & & & -30b &+& 78\cdot \left(-6\right) &=& -348 & \Rightarrow b = -4 \\ \mbox{c = -6 und b = -3 in I} & -a &-& 2\cdot \left(-4\right) &+& 7\cdot \left(-6\right) &=& -35 & \Rightarrow a = 1 \end{array}

Die Lösungsmenge lautet also \mathbb{L} &=& \{\left(1; -4; -6\right)\}

Bemerkung: Im ersten Schritt wurden nur die ersten beiden Gleichungen vertauscht, da die weiteren Umformungen mit dem Koeffizienten -1 einfacher durchzuführen sind.
zurückErklärungen 
  Aufgabenweiter