Die
allgemeine Gleichung einer quadratischen Funktion lautet:
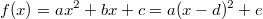
mit
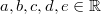
(siehe
Mengen u. a.)
Der
Graph einer quadratischen Funktion ist eine
Parabel, dabei wird der Graph der Funktion
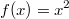 Normalparabel
Normalparabel genannt. Der auffälligste Punkt einer Parabel ist der
Scheitelpunkt: Der Scheitelpunkt einer nach oben geöffneten Parabel ist identisch mit dem tiefsten Punkt der Parabel. Bei einer nach unten geöffneten Parabel liegt der Scheitelpunkt im höchsten Punkt.
Um den Graphen einer quadratischen Funktion zu ermitteln, kann eine
Wertetabelle, in der die berechneten
Funktionswerte gesammelt werden, helfen.
Ist eine quadratische Funktion in der Form
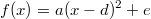
gegeben, kann man den Scheitelpunkt direkt ablesen:
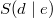
. Daher wird diese Darstellung quadratischer Funktionen auch Scheitelpunktform genannt. Auf das Minus in der Klammer aufpassen! Ist eine quadratische Funktion in ausmultiplizierter Form gegeben, muss sie erst in die obige Form gebracht werden, damit man den Scheitelpunkt ermitteln kann. Das Verfahren dazu heißt
quadratische Ergänzung und beruht auf der Anwendung der
1. und 2. Binomischen Formel von rechts nach links. Das genaue Vorgehen wird an folgendem Beispiel erklärt:
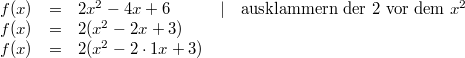
Der Term innerhalb der runden Klammer soll mithilfe der 2. Binomischen Formel zusammengefasst werden zu
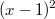
. Das funktioniert aber nicht einfach so, denn
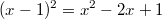
. Es stimmen zwar die ersten beiden
Summanden überein, aber das
Quadrieren mit der Binomischen Formel liefert eine
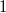
als letzten Summanden und nicht eine
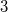
. Bekanntermaßen gilt ja aber
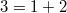
. Das fügt man in die obere Gleichung ein und erhält:
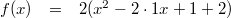
Nun hat man alle drei Summanden zusammen, um die 2. Binomische Formel von rechts nach links anwenden zu können, dabei bleibt die letzte
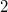
in der Gleichung übrig:
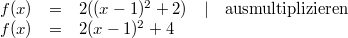
Jetzt kann man den Scheitelpunkt ablesen. Er liegt bei
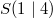
 Brückenkurs
Brückenkurs