Allgemeines
Eine quadratische Gleichung ist eine Gleichung in der folgenden Form:
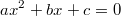
mit
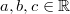
und
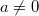
Verschiedene Lösungswege
Auch beim Lösen quadratischer Gleichungen sollen - wie beim Lösen
linearer Gleichungen - für die
Variable alle Werte gefunden werden, bei denen nach dem Einsetzen beide Seiten gleich groß sind. Die für das Auflösen linearer Gleichungen beschriebenen Schritte werden hier in ähnlicher Weise angewendet.
Es gibt verschiedene Möglichkeiten, eine quadratische Gleichung zu lösen. Grundsätzlich führen alle diese Wege zum richtigen Ergebnis. Je nach Form, in der die quadratische Gleichung vorliegt, kann aber jeweils ein anderer Weg kürzer und damit weniger fehleranfällig sein.
p-q-Formel
Eine quadratische Gleichung der Form
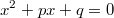
mit
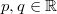
(
Normalform) lässt sich mithilfe der p-q-Formel lösen. Wichtig ist hierbei, dass der
Koeffizient von dem
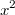
-Term
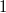
ist.
p-q-Formel: 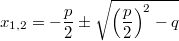 Bemerkung:
Bemerkung: Achten Sie darauf, dass
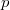
und
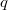
ein Vorzeichen haben können. Lautet z. B. die Gleichung
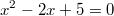
, ist
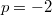
und
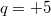
a-b-c-Formel
Eine quadratische Gleichung der Form
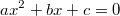
mit
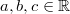
,
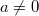
(
allgemeine Form) lässt sich mithilfe der a-b-c-Formel lösen. Alternativ kann man durch

teilen. Dann erhält man

, also die quadratische Gleichung in Normalform, sodass die p-q-Formel angewendet werden kann mit
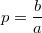
und
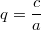 a-b-c-Formel:
a-b-c-Formel: 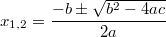
Satz vom Nullprodukt
Liegt eine quadratische Gleichung
faktorisiert vor, d. h. in der Form
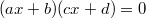
oder
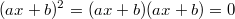
, oder lässt sie sich leicht in ein solches
Produkt umformen, hilft der
Satz vom Nullprodukt: Ein Produkt reeller Zahlen ist genau dann
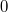
, wenn einer der
Faktoren 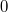
ist.
Man kann also die Terme in den Klammern separat betrachten, sodass nur noch
lineare Gleichungen zu lösen sind.
Dieser Weg ist auch zu empfehlen bei Gleichungen der Form
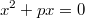
. Denn es gilt:
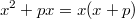
(
ausklammern).
Umformen
Bei quadratischen Gleichungen in der Form
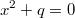
bzw.
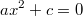
, kann man einfach den
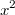
-Term auf einer Seite der Gleichung isolieren (d. h. auf dieser Seite der Gleichung darf dann nur noch
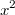
stehen, alles andere muss sich auf der anderen Seite der Gleichung befinden). Anschließend kommt man durch
Wurzelziehen zum Ergebnis der quadratischen Gleichung.
Dabei aufpassen: Auch wenn Wurzeln immer nichtnegativ sind, entstehen beim Wurzelziehen aus einer positiven Zahl
zwei Lösungen. Z. B. hat die Gleichung
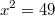
die beiden Lösungen
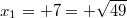
und
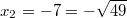
. Kurz schreibt man dafür auch gerne:
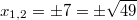
Ähnlich geht es bei einer quadratische Gleichung in Scheitelpunktform, also in der Form
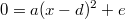
bzw.
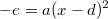
: Hier kann man die Klammer mit dem Quadrat auf einer Seite der Gleichung isolieren. Dann sieht die Gleichung so aus:
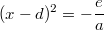
. Anschließend zieht man auf beiden Seiten die Wurzel. Das geht, wenn entweder

oder

negativ ist, weil dann
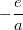
positiv ist.
Alternativ bringt man die Gleichung durch
Ausmultiplizieren bzw. Anwendung der
1. oder 2. Binomischen Formel auf eine Form, in der die a-b-c- oder die p-q-Formel angewendet werden kann.
Lösbarkeit quadratischer Gleichungen
Analog zu den
linearen Gleichungen kommt man auf die Frage: Ist jede quadratische Gleichung, also jede Gleichung der Art
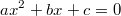
mit
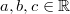
und
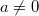
, im Bereich der
reellen Zahlen lösbar?
Für die Antwort betrachten wir beispielhaft die folgenden drei Fälle:
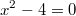
Diese quadratische Gleichung ist
lösbar und hat
zwei Lösungen. D. h., es gibt genau zwei Zahlen, die diese Gleichung lösen. Formt man sie um, erhält man nämlich
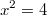
bzw.
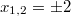
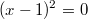
Diese quadratische Gleichung ist
lösbar und hat
eine Lösung. D. h., es gibt genau eine Zahl, die diese Gleichung löst. Formt man sie um, erhält man nämlich
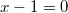
bzw.
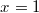
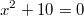
Die quadratische Gleichung ist
nicht lösbar. D. h., es gibt keine Zahl, die diese Gleichung löst. Formt man sie um, erhält man nämlich
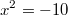
bzw.
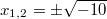
. Aus
negativen Zahlen können aber in
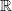
keine
Wurzeln gezogen werden.
Zusammenfassung: Quadratische Gleichung können im Bereich der reellen Zahlen
keine, eine oder zwei Lösungen haben.
 Brückenkurs
Brückenkurs