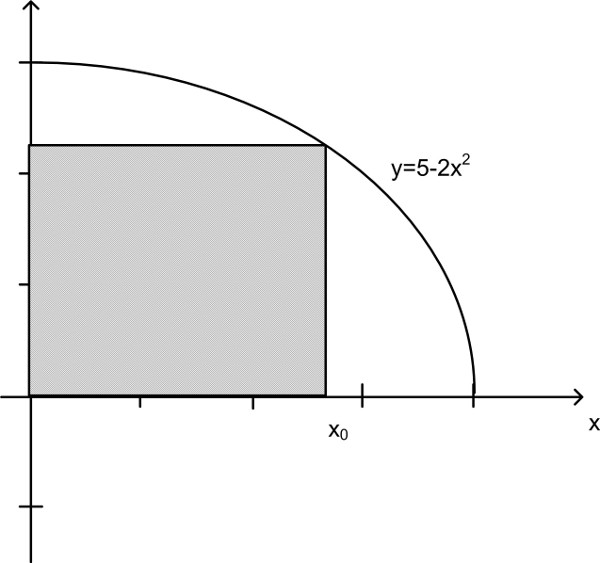
| Abbildung 62: f(x)=5−2x2 |
Extremwertaufgaben können u.U. helfen, Optima herauszufinden.
gegeben: Zielfunktion
gesucht: Minimum, Maximum.
Beispiel 13 - 30 df0780
Gegeben sei die Funktion f(x) = 5 − 2 x2. Ein Rechteck werde durch die x- und y-Achsen sowie einen Punkt der Funktion f(x) begrenzt.

Abbildung 62: f(x)=5−2x2
.
Lösung ansehen .
.
Beispiel 13 - 31 df0790
Aus einem Baumstamm mit kreisförmigem Querschnitt soll ein Balken mit rechteckigem Querschnitt so herausgeschnitten werden, daß sein Widerstandsmoment W = b · h2/6 (Breite b, Dicke h) möglichst groß wird. .
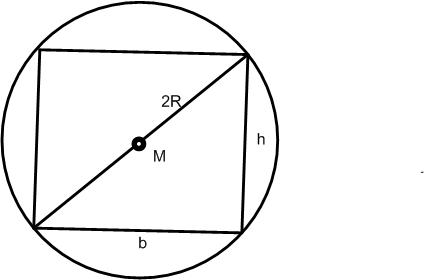
Abbildung 63: Baumstamm
Wie groß ist h bzw .b ? .
.
Lösung ansehen .
.
.
Beispiel 13 - 32
df9020 .
Gegeben ist eine Lampe mit der Lichtstärke L.
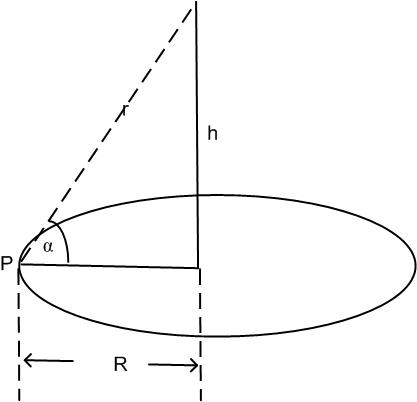
Abbildung 64: Lampe am Tisch
In Punkt P gilt für die Helligkeit:
B=L· r−2· sinα
gesucht ist die maximale Ausleuchtung des Tischrandes.
Wie hoch muss die Lampe aufgehängt werden?
.
.
Lösung ansehen .
.