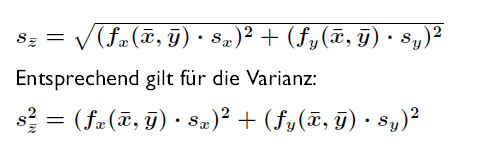20.2.2  Gaußsches Fehlerfortpflanzungsgesetz (Varianzfortpflanzungsgesetz)

Beispiel 20 - 27 st9110
Nun interessiert uns die Auswirkung der Standardabweichungen s_x und s_y der beiden unabhängigen Meßgrößen X und Y auf die Standardabweichung s_z der abhängigen indirekten Meßgröße Z =f(X;Y). .
Für die einzelnen Abweichungen gilt (s.o.): .
w_i = z_i − z = f(x_i;y_i)− f(x; ȳ) = f(x+u_i; ȳ+v_i) − f(x;ȳ) .
Die sehr kleinen Werte von w_i, u_i und v_i ersetzen wir näherungsweise durch das Differential .
d  z_i = d  f(x, ȳ)/ dx · u_i + d  f(x, ȳ)/ dy · v_i = f_x(x, ȳ) · u_i + f_y(x, ȳ) · v_i. .

w_i = d z_i= z_i − z= f_x(x, ȳ) · u_i + f_y(x, ȳ) · v_i. .
Verwendet man die Abkürzungen a= f_x(x, ȳ) und b= f_y(x, ȳ), erhält man damit .
w_i = z_i − z=au_i+bv_i. .
Die Summe der Abweichungsquadrate beträgt dann: .
.
Lösung ansehen .
.

Damit erhält man das Gaußsche Fehlerfortpflanzungsgesetz für die Standardabweichung. .
.
.
.
.
Die Streuung der Mittelwerte (die man aus mehreren Messreihen erhalten hat) um den ’wahren’ Mittelwert µ beträgt andererseits .
.
s_x= s_x/ √n, s_ȳ= s_y/ √n, s_z= s_z/ √n. .
.
Damit wird obige Gleichung zu .
.
.
.
.
.
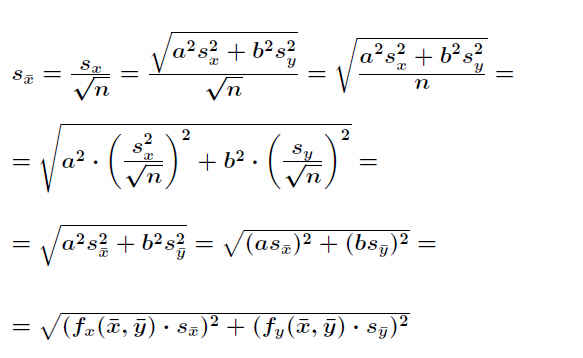Dies ist das Gaußsche Fehlerfortpflanzungsgesetz für die Standardabweichung des Mittelwerts . .
Für die Varianz gilt entsprechend: .
.
.
.
.
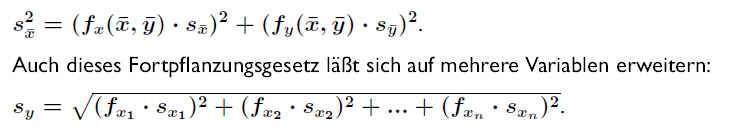Beispiel 20 - 28 st9112
Sie erhalten von Ihrem Lieferanten zylindrische Scheiben aus Metall mit der Dicke von exakt d=1 mm. Sie sollen anhand der Dichte feststellen, ob der Lieferant die Scheiben wie behauptet aus Bronze (Dichte ρ_B = 8,73 g/cm³) oder aus dem billigeren Messing (Dichte ρ_M = 8,5 g/cm³) gefertigt hat. .
Sie verfügen über eine Waage sowie über eine Schieblehre, mit der Sie die Masse bzw. den Radius r (über den Durchmesser) der Scheiben bestimmen können. Die Masse ergibt sich nach der Formel m=ρ · d · π · r². .
Die Dichte kann man damit bestimmen über die Formel .
ρ =f(m;r) = m/d · π · r² =m/ d · π · 1/r². .
Da die Messwerte aufgrund der begrenzten Genauigkeit der Messgeräte sowie wegen der Fertigungstoleranzen streuen, messen Sie die Massen m und die Radien r (halber Durchmesser) zehnmal. Wie genau kann man damit die Dichte angeben ? .
.
.

.
.
Gesucht sind also Mittelwert, Standardabweichung, Meßunsicherheit und prozentualer Fehler. .
.
.
.
Lösung ansehen .
.