Definition: Exponentialgleichungen sind
Gleichungen, bei denen die
Variable im
Exponenten einer
Potenz steht.
Sie lassen sich u. U. durch Logarithmieren der Gleichung lösen.
Definition: Logarithmusgleichungen sind Gleichungen, bei denen die Variable im
Argument eines
Logarithmus' steht.
Sie lassen sich u. U. durch Exponentieren der Gleichung lösen.
Grundsätzlich hilfreich sind in diesem Zusammenhang auch die
Potenz- und Logarithmengesetze.
Einige Exponential- und Logarithmengleichungen sind nur auf den ersten Blick wirklich schwierig. Häufig lassen sie sich nämlich mit wenigen Umformungen auf einfache
Polynomgleichungen zurückführen. Allerdings muss anschließend immer geprüft werden, ob die gefundenen Ergebnisse tatsächlich im
Definitionsbereich der ursprünglichen Gleichung liegen, vor allem wenn ein Logarithmus in der Gleichung enthalten ist!
Andere Exponential- und Logarithmengleichungen lassen sich nicht exakt sondern nur numerisch lösen.
Eine Bemerkung zu den Beispielen: Mit
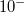
hinter dem senkrechten Strich am Ende einer Zeile soll angedeutet werden, dass beide Seiten der Gleichung die Zahl
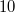
als Basis bekommen, also "
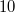
hoch" die entsprechenden Terme gerechnet wird. Mit
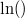
hinter dem senkrechten Strich am Ende einer Zeile ist gemeint, dass der natürliche Logarithmus auf beiden Seiten der Gleichung angewendet wird. Analog für andere Basen und andere Logarithmen.
Beispiele: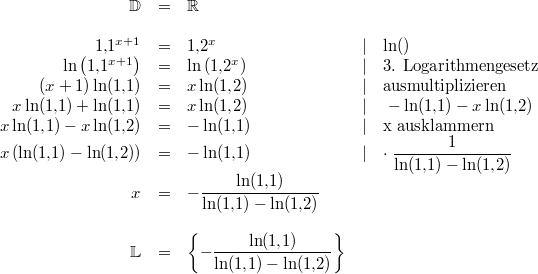 Bemerkung 1:
Bemerkung 1: 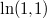
und
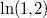
sind einfach nur Zahlen, auch wenn es auf den ersten Blick vielleicht nicht so aussieht...
Bemerkung 2: 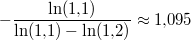
Warum ist das Ergebnis
positiv, wo doch ein Minuszeichen vor dem
Bruch steht? Ohne genaue Zahlenwerte für die Logarithmen zu ermitteln, kann man sich folgendes überlegen: Der
natürliche Logarithmus ist eine
streng monoton steigende Funktion. Das bedeutet, dass größere
Argumente zu größeren
Funktionswerten führen. Da
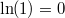
ist, muss
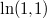
etwas größer als
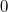
sein. Außerdem muss
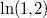
etwas größer als
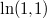
sein. Daraus folgt, dass im
Nenner des oberen Bruches eine
negative Zahl steht. Da der
Zähler positiv ist, ist der gesamte Bruch also negativ. Zusammen mit dem Minuszeichen davor ergibt sich also ein positiver Wert.
Bemerkung 3: Ob man lieber mit dem natürlichen Logarithmus oder einem Logarithmus zu einer anderen Basis rechnet, hat keinen Einfluss auf das Ergebnis.
![\begin{array}{rclcl} \mathbb{D} &=& ]-1;\infty[ \\ \\ \ln(2x) &=& \ln(x+1) &\vert& e^{-} \\ e^{\ln(2x)} &=& e^{\ln(x+1)} \\ 2x &=& x+1 &\vert& -x \\ x &=& 1 \\ \\ \mathbb{L} &=& \{1\} \end{array}](./teximg/img1355.png) Bemerkung:
Bemerkung: Hier wurde genutzt, dass
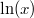
und
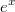
Umkehrfunktionen sind, d. h. sie sich in ihrer Wirkung aufheben. Daher ist hier die Wahl der Basis entscheidend, um die Gleichung in der oben gezeigten Weise zu vereinfachen. Nach dieser Umformung bleibt eine ziemlich simple
lineare Gleichung.
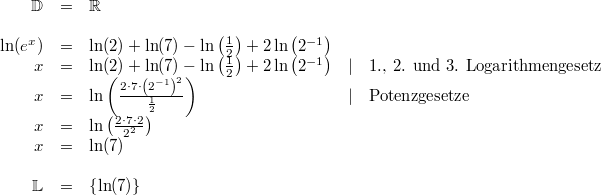 Bemerkung:
Bemerkung: Da
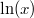
und
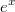
Umkehrfunktionen sind, vereinfacht sich die linke Seite der Gleichung sofort zu

. Auf der rechten Seite musste ohnehin nur zusammengefasst werden.
 Brückenkurs
Brückenkurs