Dieses Kapitel zeigt einige weitere Funktionstypen, vor allem mit dem Ziel ihre typischen Verläufe und einige Eigenschaften deutlich zu machen. Allerdings werden diese Themen nur angerissen und nicht sehr tiefgehend behandelt.
Gebrochen rationale Funktionen
Definition: Eine gebrochen rationale Funktion ist eine
Funktion von folgender Gestalt:
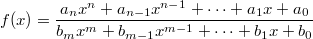
mit
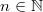
,
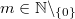
,
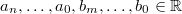
und
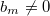 Anders formuliert:
Anders formuliert: Eine gebrochen rationale Funktion ist ein
Quotient zweier
Polynome, wobei der
Grad des Polynoms im
Nenner mindestens
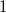
sein muss.
Das Polynom im
Zähler nennt man
Zählerpolynom. Den Grad des Zählerpolynoms nennt man
Zählergrad.
Das Polynom im Nenner nennt man
Nennerpolynom. Den Grad des Nennerpolynoms nennt man
Nennergrad.
Ganz wichtig: An den
Nullstellen des Nennerpolynoms ist eine gebrochen rationale Funktion nicht definiert, da sonst durch
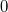
geteilt werden würde. Hier muss also viel mehr auf den
Definitionsbereich geachtet werden als bei
linearen Funktionen und Polynomen.
In der folgenden Grafik sind die Graphen der (sehr einfachen) gebrochen rationalen Funktionen
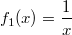
und
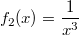
jeweils mit
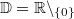
dargestellt. Solche Graphen nennt man
Hyperbeln ungerader Ordnung.
Gemeinsame Punkte: Diese ganz einfachen Hyperbeln ungerader Ordnung (also alle Funktionen der folgenden Gestalt
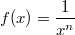
mit
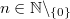
und
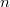
ungerade) verlaufen alle durch die Punkte
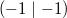
und
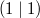 "Besondere Punkte":
"Besondere Punkte": Diese Hyperbeln haben eine
Polstelle bei
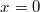
, aber keine
Nullstellen, Extrema und Wendepunkte.
Randverhalten: Die
Funktionswerte nähern sich sowohl für sehr kleine als auch für sehr große x-Werte der
an (für weitere Informationen zum
Randverhalten).
Symmetrie: Als Funktionen mit ausschließlich ungeraden Exponenten sind ihre Graphen
punktsymmetrisch zum Koordinatenursprung.
Wertebereich: Der
Wertebereich umfasst sämtliche
reellen Zahlen.
Analog dazu gibt es natürlich
Hyperbeln gerader Ordnung. In der folgenden Grafik sind die Graphen von
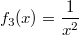
und
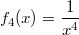
auch jeweils mit
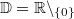
dargestellt.
Gemeinsame Punkte: Diese ganz einfachen Hyperbeln gerader Ordnung (also alle Funktionen der folgenden Gestalt
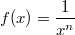
mit
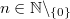
und
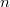
gerade) verlaufen alle durch die Punkte
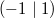
und
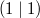 "Besondere Punkte":
"Besondere Punkte": Diese Hyperbeln haben eine Polstelle bei
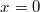
, aber keine Nullstellen, Extrema und Wendepunkte.
Randverhalten: Die Funktionswerte nähern sich sowohl für sehr kleine als auch für sehr große x-Werte der
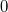
an.
Symmetrie: Als Funktionen mit ausschließlich geraden Exponenten sind ihre Graphen
achsensymmetrisch zur y-Achse.
Wertebereich: Der Wertebereich umfasst nur die
positiven reellen Zahlen.
Weitere Beispiele für gebrochen rationale Funktionen:
-
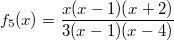 mit
mit 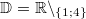
-
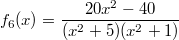 mit
mit 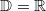
-
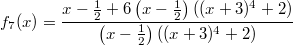 mit
mit 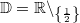
-
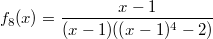 mit
mit ![\mathbb{D}=\mathbb{R}\backslash_{\left\{1-\sqrt[4]{2}; 1; 1+\sqrt[4]{2}\right\}}](./teximg/img1386.png)
Sie sehen in den Grafiken, dass der Verlauf von komplexeren gebrochen rationalen Funktionsgraphen recht unterschiedlich sein kann.
"Besondere Punkte": Gebrochen rationale Funktionen können an den Nullstellen des Nennerpolynoms (also an den Definitionslücken)
Polstellen haben oder auch nicht (das hängt davon ab, ob das Zählerpolynom an dieser Stelle auch eine Nullstelle hat). Eine gebrochen rationale Funktion kann
Nullstellen haben und zwar an den Nullstellen des Zählerpolynoms. Allerdings muss eine Nullstelle des Zählerpolynoms nicht zwangsläufig eine Nullstelle der gesamten Funktion bewirken (das wiederum hängt davon ab, ob das Nennerpolynom an dieser Stelle eine Nullstelle hat). Ob eine gebrochen rationale Funktion
Extrema und
Wendepunkte hat, kann man nicht im Allgemeinen sagen.
Randverhalten: Ob sich die Funktionswerte für sehr kleine und sehr große x-Werte der
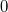
oder einer anderen reellen Zahl annähern oder sehr groß bzw. sehr klein werden, hängt vom Verhältnis von Zähler- zu Nennergrad ab.
Wertebereich: Der Wertebereich kann sämtliche reellen Zahlen oder nur Teilbereiche von ihnen umfassen.
Wichtige Bemerkung: Die Funktion
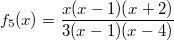
ist nicht identisch mit der Funktion
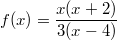
, da sich der Definitionsbereich ändert. Es darf also nicht einfach so gekürzt werden.
Wurzelfunktionen
Definition: Eine Wurzelfunktion ist eine Funktion, bei der die
Variable "unter einer
Wurzel" steht, also
![f(x)=\sqrt[n]{x}](./teximg/img1388.png)
mit
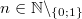
und
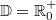
, da im Bereich der
reellen Zahlen aus
negativen Zahlen keine Wurzeln berechnet werden können.
Beispiele: Die Graphen sehen Sie in der nächsten Grafik.
Gemeinsamer Punkt: Diese einfachen Wurzelfunktionen verlaufen alle durch den Punkt
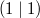 "Besondere Punkte":
"Besondere Punkte": Sie haben eine Nullstelle bei
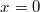
, aber keine Polstellen, Extrema und Wendepunkte.
Symmetrie: Aufgrund des eingeschränkten Definitionsbereichs können die Graphen von Wurzelfunktionen nicht symmetrisch sein.
Wertebereich: Der Wertebereich umfasst nur die
nichtnegativen reellen Zahlen.
Wurzelfunktionen wachsen zwar langsamer als alle Polynomfunktionen, auch als
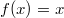
, aber immer noch schneller als Logarithmusfunktionen.
Betragsfunktionen
Definition: Eine Betragsfunktion ist eine Funktion, bei der auf einen
Term, der die Variable enthält, ein
Betrag angewendet wird.
In der folgenden Grafik sind die Funktionen
dargestellt.
"Besondere Punkte": Bei einfachen Betragsfunktionen sind alle Nullstellen zugleich Minima.
Wertebereich: Der Wertebereich umfasst nur die nichtnegativen reellen Zahlen.
Sonstiges: Typisch für eine Funktion, die einen Betrag enthält, ist ein "Knick" im Funktionsgraphen, der sich ergibt, wenn die Ursprungsfunktion (also die Funktion ohne den Betrag) positive
und negative Funktionswerte hatte. Auf diesen "Knick" muss z. B. bei der
Differenzialrechnung besonders geachtet werden.
Abschließendes
Sowohl Wurzel- als auch Betragsfunktionen können nach oben/unten und links/recht
verschoben sowie
gestreckt oder
gestaucht werden, so wie Sie das von
Parabeln kennen. Dann ändern sich natürlich auch die oben aufgeführten Eigenschaften und speziellen Punkte entsprechend. Betrachten Sie bespielsweise die Funktion
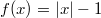
(siehe folgende Grafik): Obwohl ein Betrag enthalten ist, gilt
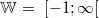
. Außerdem hat die Nullstellen bei
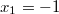
und
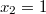
, ihr Minimum allerdings bei
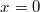
. Das liegt daran, dass der Betrag nicht den gesamten Funktionsterm umfasst.
 Brückenkurs
Brückenkurs