Allgemeines
Allgemeine Darstellung eines Polynoms:
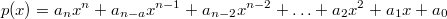
, mit
,
und
(siehe
Mengen u. a.)
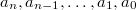
heißen
Koeffizienten des Polynoms.
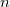
heißt
Grad des Polynoms.
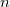
ist aber nur dann tatsächlich der Grad des Polynoms, wenn
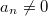
ist.
Bemerkung 1: Polynome werden auch als
ganz rationale Funktionen bezeichnet. Natürlich können sie auch
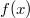
heißen.
Bemerkung 2: Da die Koeffizienten in Polynomen Elemente der
reellen Zahlen sind, sind selbstverständlich auch
Bruchzahlen als Koeffizienten möglich. Die
Variable in einem Polynom darf aber nicht im
Nenner eines Bruches stehen.
Bemerkung 3: Bei klassischen Polynomen kommen als
Definitionsbereich üblicherweise die gesamten
reellen Zahlen infrage.
Beispiele
: Hier sind die Koeffizienten:
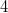
,
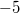
,
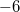
und
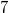
. Der Grad ist
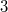
.
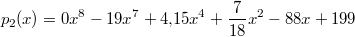
: Hier sind die Koeffizienten:
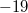
,
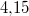
,
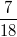
,
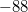
und
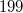
. Der Grad ist
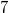
, da der Koeffizient von
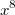
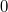
ist.
Spezielle Polynome
Einige häufig auftretende Polynome haben
spezielle Bezeichnungen:
Bemerkung 1: Nur bei linearen, quadratischen und biquadratischen Polynomen existieren einfache Lösungsalgorithmen zur Berechnung von
Nullstellen. Bei Polynomen dritten, vierten oder höheren Grades kann das Finden von Nullstellen sehr aufwändig bzw. nur noch näherungsweise möglich sein.
Bemerkung 2: Die Anzahl der Nullstellen eines Polynoms ist im Bereich der
reellen Zahlen (
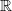
) maximal so groß wie der Grad des Polynoms. Polynome ungeraden Grades haben immer mindestens eine Nullstelle. Beispiele: Ein Polynom zweiten Grades kann keine, eine oder zwei Nullstellen haben. Ein Polynom dritten Grades kann eine, zwei oder drei Nullstellen haben.
Ein
Parameter ist eine spezielle
Variable. Sie unterscheidet sich von "normalen" Variablen dadurch, dass sie in einer Rechnung als konstant angenommen wird. Man kann in der Rechnung den Parameter wie eine Zahl behandeln - nur dass man nicht weiß, um welche Zahl es sich genau handelt.
Eigenschaften von Polynomen
Bitte beachten Sie: Bei den folgenden Ausführungen fehlen größtenteils die mathematischen Begründungen, da diese über den Umfang des Brückenkurses hinausgehen. Sie werden sich im Studium mit diesen auseinandersetzen.
Symmetrie
Polynome mit ausschließlich
geraden Exponenten (auch "gerade Polynome" genannt) sind
achsensymmetrisch zur y-Achse, da solche Polynome die Bedingung für Achsensymmetrie zur y-Achse
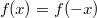
immer erfüllen.
Polynome mit ausschließlich
ungeraden Exponenten (auch "ungerade Polynome" genannt) sind
punktsymmetrisch zum Koordinatenursprung, da solche Polynome die Bedingung für Punktsymmetrie zum Koordinatenursprung
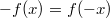
immer erfüllen.
Polynome mit
beliebigen Exponenten sind weder achsensymmetrisch zur y-Achse noch punktsymmetrisch zum Koordinatenursprung, können aber zu anderen Geraden bzw. Punkten symmetrisch sein.
In der folgenden Grafik sind die Funktionen
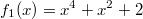
(gerades Polynom),
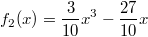
(ungerades Polynom) und
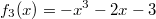
dargestellt. Bitte beachten Sie:
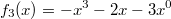
. Damit ist
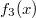
kein Polynom mit ausschließlich ungeraden Exponenten und entsprechend nicht punktsymmetrisch zum Ursprung. Es ist allerdings punktsymmetrisch zum Punkt
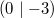
Randverhalten
Diese Erklärungen gehen davon aus, dass die Polynomfunktionen für die gesamten
reellen Zahlen, also von
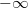
bis
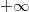
, definiert sind. Da beim Randverhalten (wie der Name schon sagt) nur das Verhalten an den Rändern des
Definitionsbereichs interessiert, wird hier nichts über den Verlauf "dazwischen" ausgesagt.
Bei Polynomen
geraden Grades sind zwei Verläufe denkbar: Entweder liefern sowohl sehr kleine x-Werte als auch sehr große x-Werte sehr große
Funktionswerte oder sowohl sehr kleine x-Werte als auch sehr große x-Werte liefern sehr kleine Funktionswerte. "Sehr klein" bedeutet dabei, dass es sich um
negative Zahlen mit einem sehr großen
Betrag handelt.
Welche der beiden Varianten vorliegt, hängt davon ab, welches Vorzeichen der
Koeffizient der höchsten
Potenz hat. Ist dieser Koeffizient
positiv, folgt die Funktion dem ersten beschriebenen Verlauf, bei einem
negativen Koeffizienten dem zweiten Verlauf.
In der folgenden Grafik sind die Funktionen
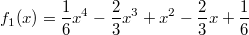
und
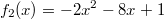
abgebildet.
Auch für Polynome
ungeraden Grades gibt es zwei mögliche Verläufe: Ist der Koeffizient der höchsten Potenz positiv, sind die Funktionswerte für sehr kleine x-Werte ebenfalls sehr klein. Die Funktionswerte für sehr große x-Werte werden sehr groß. Bei einem negativen Koeffizienten der höchsten Potenz sind die Funktionswerte für sehr kleine x-Werte sehr groß und für sehr große x-Werte sehr klein.
In der folgenden Grafik sind die Funktionen
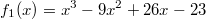
und
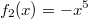
zu sehen.
Nullstellen
Grundsätzlich gilt: Polynome vom Grad
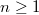
haben im Bereich der
reellen Zahlen maximal
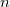 Nullstellen
Nullstellen.
In der Grafik sind verschiedene Varianten der Funktion
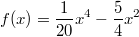
dargestellt. Abhängig von der Konstanten, die zu diesem Funktionsterm
addiert wird, ändert sich die Zahl der Nullstellen:
- Die oberste der abgebildeten Funktionen
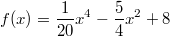 hat keine Nullstellen.
hat keine Nullstellen.
- Die an zweiter Stelle abgebildete Funktion
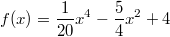 hat vier Nullstellen.
hat vier Nullstellen.
- Die an dritter Stelle abgebildete Funktion
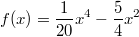 hat drei Nullstellen.
hat drei Nullstellen.
- Die unterste der abgebildeten Funktionen
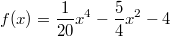 hat zwei Nullstellen.
hat zwei Nullstellen.
Polynome
ungeraden Grades haben mindestens eine Nullstelle. Wenn Sie sich an das Randverhalten von Polynomen ungeraden Grades erinnern, dürfte dies anschaulich klar sein.
In der folgenden Grafik sind verschiedene Varianten der Funktion
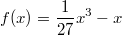
dargestellt. Abhängig von der Konstanten, die zum Funktionsterm addiert wird, ändert sich auch hier die Zahl der Nullstellen. Allerdings bewirkt keine Konstante, dass die Funktion vollständig über oder vollständig unter der
x-Achse liegt:
- Die oberste der abgebildeten Funktionen
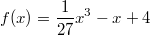 hat eine Nullstelle.
hat eine Nullstelle.
- Die mittlere der abgebildeten Funktionen
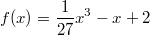 hat zwei Nullstellen.
hat zwei Nullstellen.
- Die unterste der abgebildeten Funktionen
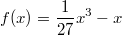 hat drei Nullstellen.
hat drei Nullstellen.
Extrema
Polynome vom Grad
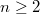
haben im Bereich der reellen Zahlen maximal
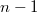
Extrema.
Allgemein lässt sich zur Lage von Extrema sagen, dass zwischen zwei Maxima immer ein Minimum und zwischen zwei Minima immer ein Maximum liegen muss. Zwischen zwei Nullstellen muss sich immer ein Extremum befinden (Dies gilt
mit Ausnahme der Funktion
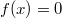
). Umgekehrt liegt ein Extremum aber
nicht immer automatisch zwischen zwei Nullstellen.
Bei Polynomen
geraden Grades existiert mindestens ein Extremum.
Wende- und Sattelpunkte
Polynome vom Grad
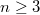
haben im Bereich der reellen Zahlen maximal
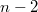
Wendepunkte.
Klar ist: Zwischen zwei Extrema muss sich immer ein Wendepunkt befinden. Allerdings müssen Wendepunkte nicht zwischen Extrema liegen.
Polynome
ungeraden Grades haben mindestens einen Wendepunkt.
In der folgenden Grafik sind die Funktionen
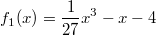
(
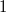
Nullstelle,
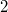
Extrema,
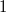
Wendepunkt) und
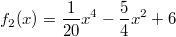
(
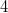
Nullstellen,
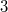
Extrema,
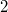
Wendepunkte) dargestellt.
Polstellen
Polynome haben keine Polstellen.
 Brückenkurs
Brückenkurs