Erklärungen
In Kapitel 5 hatten wir Gleichungen
eingeführt als "ein Term = ein
(anderer) Term". Ganz ähnlich funktioniert es für
Ungleichungen. Allerdings gibt es hier vier Varianten:
- "ein
Term
 ein (anderer) Term"
ein (anderer) Term"
- "ein
Term
 ein (anderer) Term"
ein (anderer) Term"
- "ein
Term
 ein (anderer) Term"
ein (anderer) Term"
- "ein
Term
 ein (anderer) Term"
ein (anderer) Term"
Die Vergleichszeichen
oder auch Relationszeichen heißen:
-
Kleinerzeichen:
 (gesprochen: "kleiner als", manchmal auch "echt
kleiner als")
(gesprochen: "kleiner als", manchmal auch "echt
kleiner als")
-
Kleinergleichzeichen:
 (gesprochen: "kleiner gleich")
(gesprochen: "kleiner gleich")
-
Größerzeichen:
 (gesprochen: "größer als", manchmal auch "echt
größer als")
(gesprochen: "größer als", manchmal auch "echt
größer als")
-
Größergleichzeichen:
 (gesprochen: "größer gleich")
(gesprochen: "größer gleich")
Merke:
Die Vergleichszeichen sind immer zur größeren Seite
geöffnet.
Auch "ein Term 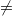
ein (anderer) Term" (mit dem Ungleichheitszeichen 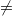 ) ist
natürlich eine Ungleichung. Allerdings wird sie meist
nicht gesondert behandelt, weil man ja nur die
zugehörige Gleichung lösen muss. Alles, was dabei nicht
Lösung ist,
ist dann Lösung der Ungleichung.
Wie bei Gleichungen ist es auch bei Ungleichungen
meist die Aufgabe, diejenigen Werte der Variablen
zu ermitteln, für die die Ungleichung wahr wird.
Anders formuliert: Man möchte die Lösungen der
Ungleichungen finden. Grundsätzlich behandelt
man Ungleichungen genauso wie Gleichungen, nämlich mit
Äquivalenzumformungen.
Allerdings gibt es einige wenige Unterschiede zu
beachten:
-
Vertauscht man die beiden Seiten einer
Ungleichung, muss auch das Vergleichszeichen
"umgedreht" werden. Ein (einfaches) Beispiel: Aus
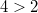 wird
naheliegenderweise wird
naheliegenderweise 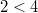
- Bei Multiplikation
mit negativen
Zahlen muss das Vergleichszeichen ebenfalls
"umgedreht" werden. Dies schließt die Division mit ein.
Beispiel: Aus
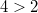 wird
wird 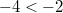
- Sind
beide Seiten einer Ungleichung positiv (bzw.
negativ) führt auch die Bildung von Kehrwerten dazu, dass
das Vergleichszeichen "umgedreht" werden muss.
Haben beide Seiten unterschiedliche Vorzeichen,
bleibt das Vergleichszeichen, wie es ist.
Beispiele: Aus
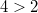 folgt
folgt 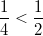 ,
aber bei ,
aber bei 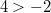 gilt
gilt 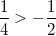
Diese Regeln gelten natürlich auch für die anderen
Vergleichszeichen und wenn Variablen etc. in der
Ungleichung enthalten sind. Dann ist es allerdings
meist nicht mehr ganz so offensichtlich wie hier...
Nur der Sicherheit halber sei nochmal betont, dass
natürlich auch bei Ungleichungen alle Umformungen auf
beiden
Seiten durchgeführt werden müssen, damit sich die Lösungsmenge
nicht ändert.
Randbemerkung:
Da in diesem Lernmodul nur recht einfache
Ungleichungen behandelt werden, reichen die oben
genannten Fälle, bei denen das Vergleichszeichen
"umgedreht" werden muss, aus. Werden die Ungleichungen
anspruchsvoller, kommen weitere Umformungen hinzu,
nämlich jene, die auf der Anwendung streng
monoton fallender Funktionen
beruhen. Außerdem muss dann überlegt werden, was bei
Funktionen, die nicht streng monoton sind, passiert.
Aber das ist ein anderes Kapitel...
Ein paar Worte zur Lösungsmenge einer
Ungleichung: Auch hier zeigt sich ein
Unterschied zu Gleichungen. Während "normal lösbare"
Gleichungen, wie sie in diesem Lernmodul betrachtet
wurden, eine endliche Anzahl von Lösungen haben (z. B.
quadratische
Gleichungen mit einer oder zwei Lösungen),
umfasst die typische Lösungsmenge bei Ungleichungen
unendlich viele Zahlen. Das liegt daran, dass in
Ungleichungen Größenvergleiche formuliert werden, also
alle Zahlen gesucht werden, die kleiner (oder größer)
als etwas Anderes sind und davon gibt es meistens eine
ganze Menge... Betrachtet man Ungleichungen im Bereich
der reellen Zahlen
ist die Lösungsmenge meist ein Intervall.
In vielen Fällen ist es eine sehr sinnvolle Idee, die
Lösungsmenge auf dem Zahlenstrahl zu veranschaulichen.
Beispiele und
Lösungsstrategien für verschiedene Arten von
Ungleichungen
Im Folgenden werden
anhand von Beispielen Lösungsstrategien für
verschiedene Arten von Ungleichungen eingeführt. Wenn
Sie Schwierigkeiten haben, die Ungleichungsarten zu
erkennen und auseinanderzuhalten, schauen Sie bitte in
den entsprechenden Gleichungskapiteln nach.
Quadratische Ungleichungen sind aus den gleichen
Gründen "quadratisch" wie quadratische Gleichungen...
Lineare Ungleichungen
Zunächst also lineare
Ungleichungen:
1.
Beispielaufgabe:
Bei einer Matheklausur gibt es pro richtiger Aufgabe 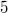 Punkte. Vorab
konnten 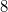
Bonuspunkte erarbeitet werden. Wie viele Aufgaben
müssen mindestens richtig gelöst werden, wenn zum
Bestehen 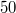
Punkte nötig sind?
Anmerkung:
Wir gehen der Einfachheit halber davon aus, dass es
keine Teilpunkte für halbrichtig gelöste Aufgaben
gibt.
Lösung:
Zu lösen ist die Ungleichung 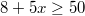 , wobei für  nur natürliche
Zahlen größer 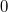
eingesetzt werden dürfen, weil ja keine Teilpunkte
vergeben werden und wir davon ausgehen können, dass
die Klausur aus mindestens einer Aufgabe besteht.
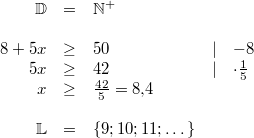 Bemerkung:
Bemerkung:
Sie sehen, dass der Lösungsweg quasi identisch zum
Lösungsweg der entsprechenden linearen
Gleichung ist. Wichtig ist noch, die 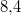 auf 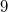 aufzurunden
aufzurunden,
weil ja nur natürliche Zahlen als Lösungen
zugelassen waren. Es muss trotz der 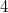
in der Nachkommastelle aufgerundet werden, weil ja
nach "mindestens" gefragt war.
Abwandlung
der 1. Beispielaufgabe:
Wie ändert sich die Lösung, wenn Sie erfahren, dass
die Klausur 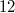
Aufgaben umfasst?
Lösung:
Die zu lösende Gleichung inklusive Lösungsweg bleibt
gleich, weil sich an der Punkteverteilung ja nichts
geändert hat. Was sich ändert, ist der Definitionsbereich:
Es kommen nun nicht mehr alle natürlichen Zahlen
größer 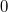 als
Lösungen infrage, sondern nur noch die natürlichen
Zahlen zwischen 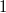
und 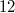
(jeweils eingeschlossen). Formal geschrieben lautet
der Definitionsbereich also: 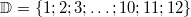
Das hat (natürlich) Auswirkungen auf die Lösungsmenge:
Berechnet haben wir, dass Zahlen größer oder gleich 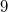 die Ungleichung
erfüllen. Davon gibt es im Definitionsbereich aber gar
nicht so viele, nämlich nur 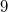 ,
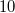 , 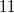 und 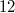
. Da nur Zahlen, die im Definitionsbereich liegen,
überhaupt als Lösungen infrage kommen, lautet die
Lösungsmenge also: 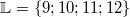 2.
Beispielaufgabe:
2.
Beispielaufgabe:
Zu lösen ist 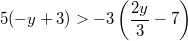 mit 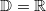 Lösung:
Lösung:
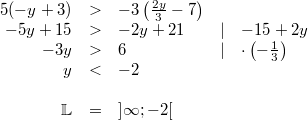 Bemerkung
1: Ganz wichtig:
Bemerkung
1: Ganz wichtig: Bei der Umformung zur
letzten Zeile muss das Vergleichszeichen "umgedreht"
werden, weil mit einer negativen
Zahl multipliziert
wurde!
Bemerkung
2: Wir haben berechnet, dass alle Zahlen aus
dem Definitionsbereich, die kleiner sind als 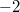 , die Ungleichung lösen.
Die Lösung ist also ein Teilbereich der reellen
Zahlen, was man am besten als Intervall
aufschreibt. Nach unten gibt es dabei keine Grenze.
Mathematisch schreibt man dafür 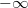
. Wichtig ist auch, dass die 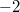 nicht
nicht
Teil der Lösungsmenge ist, weil in der letzten Zeile
der Rechnung ein Kleiner- und kein
Kleinergleichzeichen steht.
Quadratische
Ungleichungen
Es gibt
verschiedene Wege, quadratische
Ungleichungen zu lösen. Wir beschränken uns hier auf
einen, der relativ anschaulich ist und sich leicht auf
weitere Arten von Ungleichungen übertragen lässt.
Beispielaufgabe:
Zu lösen ist 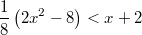 mit 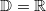 Lösung:
Lösung:
Wir betrachten die linke und die rechte Seite der
Ungleichung jeweils als Funktion,
also 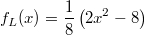 und 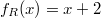 und zeichnen die
zugehörigen Graphen in
ein Koordinatensystem
(links). Gleichzeitig kann man die Ungleichung so
umformen, dass auf der rechten Seite nur noch 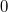 steht: 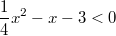 und ebenfalls den
Graphen zur dazu passenden Funktion 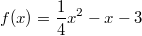 zeichnen
(Koordinatensystem rechts). Das sieht dann so aus: Man sieht in der
linken Grafik, dass 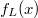
zwischen 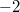
und 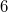 kleiner
als 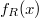
ist. Die Lösungsmenge
lautet daher 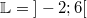 (Es handelt sich um ein
offenes
Intervall, was daran liegt, dass die Ungleichung
ein Kleiner- und kein Kleinergleichzeichen enthält.).
Alternativ suchen wir in der rechten Grafik den
Bereich, in dem 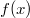
kleiner als 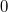
ist. Die Lösung der
Ungleichung lässt sich also direkt aus der Grafik
ablesen - mit der Einschränkung, dass das
natürlich nur funktioniert, wenn die Schnittpunkte
bei "glatten" Zahlenwerten liegen (werden wir gleich
bestätigen). Lägen die Schnittpunkte z. B. bei 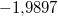 und 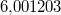 , hätten wir mit dieser
Methode keine Chance... Trotzdem lohnen sich
Zeichnungen in vielen Fällen, vor allem auch bei
komplizierteren Ungleichungen, weil man dadurch
zumindest eine Idee bekommt, wie die Lösung aussehen
muss.
Rechnerisch
nähern wir uns der Lösung, indem wir die zugehörige quadratische
Gleichung betrachten, am geschicktesten direkt
von der bereits umgeformten Ungleichung: 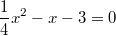 . Darüber lassen sich
nämlich die Stellen, an denen  Nullstellen
Nullstellen
hat, was ja den Rändern des Lösungsintervalls
entspricht, exakt ermitteln. Wie man oben in der
rechten Grafik sieht, ist die Funktion zwischen zwei
Nullstellen entweder immer positiv
oder immer negativ.
D. h., wir müssen dann nur noch untersuchen, welcher
Fall in welchem Teilintervall eintritt (Kleine
Einschränkung: Das funktioniert nicht, wenn die
Funktion Sprungstellen etc. haben sollte, aber solche
Funktionen betrachten wir hier nicht.). Also:
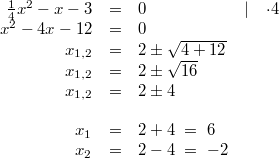
Diese Werte liefern uns drei Intervalle:
Von 
bis zur ersten Nullstelle: 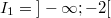
Zwischen den Nullstellen: 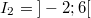
Von der zweiten Nullstelle bis 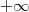
: 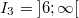 Bemerkung
1:
Bemerkung
1: 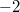
und 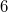 werden
nicht in die Intervalle eingeschlossen, weil wir ja
gerade berechnet haben, dass dort 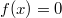
gilt. Gleichheit war aber in der ursprünglichen
Ungleichung nicht gefragt. Bei Ungleichungen, die ein
Kleinergleich- oder Größergleichzeichen enthalten,
müssten die Nullstellen in die Intervalle
eingeschlossen werden.
Bemerkung
2: Diese Dreiteilung des
Lösungsbereiches ist typisch für quadratische
Ungleichungen. Wenn Sie sich an den klassischen
Verlauf von Parabeln
erinnern, wissen Sie auch warum. Die Lösung besteht
dann entweder aus dem mittleren Intervall oder den
beiden äußeren.
Nun müssen wir noch überprüfen, wo 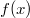
größer als 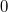
und wo 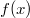
kleiner als 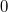
ist, denn das war ja die eigentliche Frage.
(Letztendlich kann man das natürlich auch aus den
Grafiken oben ablesen, aber hier soll ein
vollständiger Rechenweg gezeigt werden.) Das machen
wir, indem wir einzelne Werte aus den drei Intervallen
einsetzten. Welche Zahlen wir dabei nehmen, ist egal,
denn innerhalb der Intervalle gibt es ja entweder nur
positive oder nur negative Funktionswerte.
Sie dürfen sich also jeweils eine Zahl aussuchen, mit
der es sich besonders schön weiterrechnet.
Für 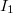 nehmen
wir 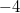 : 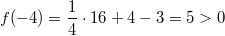
Also kommt 
nicht als Lösung infrage.
Für  nehmen
wir 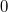 : 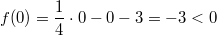 Hier passt es: 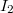 kommt als Lösung
infrage.
Für 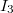 nehmen
wir 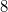 : 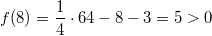 Also kommt 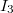 auch nicht als Lösung
infrage.
Die Lösung ist also 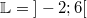 Bemerkung:
Bemerkung:
Warum gerade diese Zahlen? 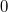
ist eigentlich immer eine gute Option, weil damit alle
Produkte wegfallen. 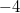
und 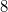 haben
den Vorteil, dass sie die betragsmäßig
kleinsten Zahlen aus den beiden Intervallen sind, die
quadriert
durch 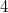 teilbar teilbar
sind. Anders gesagt: Für diese Zahlen liefert 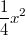 eine ganze
Zahl und keinen Bruch. Man
könnte für 
natürlich auch mit 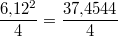 oder mit 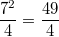 weiter rechnen, wäre
vollkommen korrekt - aber wenn die Alternative 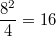 ist...
Betragsungleichungen
Zum Lösungen von
Ungleichungen, die Terme mit
Beträgen
enthalten, braucht man sogenannte Fallunterscheidungen,
denn der Betrag ist ja unterschiedlich definiert, je
nachdem, ob der Term im Betrag positiv
bzw.  oder negativ
ist. Bei Zahlen lässt sich das ja ohne Weiteres
entscheiden, sodass der Betrag dann leicht berechnen
werden kann. Durch die Variablen
ist das hier nicht ganz so einfach.
Beispielaufgabe:
Schauen wir uns 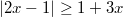 an.
Lösung:
Will man diese Ungleichung lösen, muss man den Betrag
auflösen. Dabei hilft die Definition des Betrages:
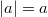
, wenn 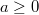
und
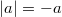
, wenn 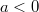
Da wir nicht wissen können, ob 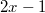
negativ oder nichtnegativ
ist, schauen wir uns einfach beide Fälle separat an.
Das nennt man eine Fallunterscheidung.
1.
Fall: Wir nehmen an 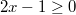
oder alternativ 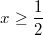
(was das gleiche ist, nur ein bisschen umgeformt).
Jetzt greift nämlich die erste Zeile der
Betragsdefinition: Da der Term im Betrag in diesem
Fall positiv ist, dürfen die Betragsstriche
weggelassen werden. Dadurch vereinfacht sich die
Ungleichung zu
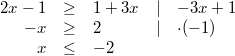
Das sieht nach einem schönen Ergebnis aus - ist es
aber leider nicht. Wir hatten ja oben bei der
Fallunterscheidung angenommen, dass 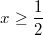 . Das bedeutet, dass nur
solche Zahlen überhaupt als Lösungen
infrage kommen. Die Frage, die nun noch beantwortet
werden muss, ist also: Gibt es Zahlen für die beide
Bedingungen gelten? Oder konkret für dieses Beispiel:
Gibt es Zahlen, die kleiner oder gleich 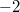 und und größer oder
gleich 
sind? Eindeutige Antwort: Solche Zahlen kann es nicht
geben! Sie müssten ja gleichzeitig positiv und negativ
sein... Also gibt es im 1. Fall keine Lösungen: 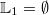 2.
Fall:
2.
Fall: Wir nehmen an 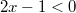
oder alternativ 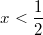
(auch hier nur ein bisschen umgeformt). Hier müssen
wir die zweite Zeile der Betragsdefinition anwenden:
Wir schreiben ein Minuszeichen vor den Term und dürfen
dafür die Betragsstriche weglassen. Wichtig ist, an
die Klammern
zu denken, weil sich das Minuszeichen ja auf den
gesamten Term auswirken soll. Dadurch vereinfacht sich
die Ungleichung zu
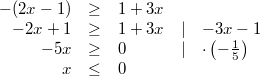
Auch nun müssen wir natürlich das Rechenergebnis mit
der Bedingung, die sich aus der Fallunterscheidung
ergeben hat, abgleichen, um eine Aussage über Lösungen
treffen zu können. Beide Bedingungen müssen erfüllt
sein. Frage: Gibt es Zahlen, die sowohl kleiner als  als
auch kleiner oder gleich 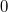
sind? Hier haben wir Glück, denn alle Zahlen, die
kleiner oder gleich 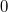
sind, sind natürlich auch kleiner als  . Die Lösungsmenge
lautet hier: 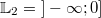 Letzter
Schritt:
Letzter
Schritt: Um zur Lösungsmenge der
ursprünglichen Ungleichung zu kommen, müssen die
beiden Teillösungsmengen zusammengefügt werden. Das
tut man mathematisch, indem man die Vereinigungsmenge
der beiden Mengen bildet:
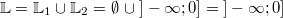 Bemerkung:
Bemerkung:
Das Bilden der Vereinigungsmenge ist bei dieser
Aufgabe ein bisschen witzlos, weil 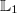 ja leer
ist. Es können zu 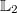
also gar keine Elemente hinzukommen. Trotzdem gehört
dieser Schritt zum vollständigen Lösungsweg dazu.
Meist hat man es ja auch mit Teillösungsmengen zu tun,
bei denen sich das vereinigen lohnt...
Noch ein paar Worte
zu Fallunterscheidungen
Fallunterscheidungen
sind grundsätzlich nichts Geheimnisvolles oder
Schlimmes. Sie sind dazu da, verschiedene Fälle, in
denen unterschiedlich weiter gerechnet oder
argumentiert werden muss, voneinander zu trennen.
Vergisst man das, entstehen üblicherweise Fehler, weil
man zu viele Dinge über einen Kamm schert. Multipliziert
man beispielsweise eine Ungleichung mit der Variablen
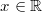
, kann man nicht wissen, ob das Vergleichszeichen
"umgedreht" werden muss oder nicht, weil man ja nicht
weiß, ob  positiv positiv
oder negativ
ist. Es könnte sogar sein, dass die Multiplikation
überhaupt nicht zulässig ist, nämlich wenn 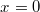 gilt. Ohne
Fallunterscheidung "verliert" man dadurch entweder
Lösungen oder man hat am Ende zu viele - beides nicht
gut... Eine saubere Fallunterscheidung führt zudem
dazu, dass die Aufgabe danach einfacher ist als
vorher. Beispielsweise hat die Fallunterscheidung bei
der letzten Beispielaufgabe oben dazu geführt, dass
wir keinen Betrag
mehr in der Ungleichung hatten. Es blieben zwei kleine
lineare
Ungleichungen übrig, die in wenigen Schritten gelöst
werden konnten.
Natürlich kann es Aufgaben geben, bei denen mehr als
zwei Fälle unterschieden werden müssen. Das
funktioniert vom Prinzip her genauso.
Zwei Dinge müssen allen Fallunterscheidungen beachtet
werden:
- Es muss
jeder Wert aus dem Definitionsbereich
in der Fallunterscheidung beachtet werden. Zum
Beispiel hatten wir oben
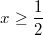 und und 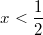 , was demnach eine
gute Fallunterscheidung ist, weil jede reelle Zahl
entweder größer bzw. gleich , was demnach eine
gute Fallunterscheidung ist, weil jede reelle Zahl
entweder größer bzw. gleich  oder kleiner als oder kleiner als  ist. Hätten wir stattdessen
ist. Hätten wir stattdessen 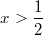 und und 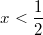 gewählt, wäre keine
Aussage über gewählt, wäre keine
Aussage über 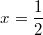 möglich gewesen. Umgekehrt wäre die Zahl
möglich gewesen. Umgekehrt wäre die Zahl  bei bei 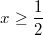 und und 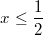 doppelt
berücksichtigt gewesen, was zu Widersprüchen
führen kann. doppelt
berücksichtigt gewesen, was zu Widersprüchen
führen kann.
- Nach der
Fallunterscheidung sind jeweils alle
Rechenoperationen und Argumentationen, die mit
dieser Voraussetzung arbeiten, erlaubt. Beispiel:
Wird bei einer Fallunterscheidung angenommen, dass
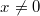 ist, darf anschließend bedenkenlos durch
ist, darf anschließend bedenkenlos durch  geteilt werden, weil
eine Division
durch geteilt werden, weil
eine Division
durch 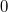 ja
ausgeschlossen ist. ja
ausgeschlossen ist.
|
 Brückenkurs
Brückenkurs