ErklärungenWas ist eine Ableitung?Die Ableitung 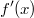 (gesprochen: "f Strich von x") einer Funktion 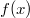 ist (vorausgesetzt die Ableitung existiert, siehe unten) die Funktion, die die Steigung der Funktion 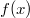 beschreibt. Eine exakte Erklärung des Begriffs "Ableitung" erfordert die Betrachtung von Grenzwerten. Da die Ableitung einer Funktion 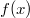 (so sie existiert) wieder eine Funktion ist, nämlich 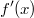 , kann sie erneut abgeleitet werden. So erhält man die zweite Ableitung 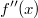 . Leitet man diese wieder ab, kommt man zur dritten Ableitung 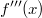 . 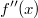 und 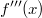 werden auch höhere Ableitungen oder Ableitungen höherer Ordnung genannt. Die Steigung der Funktion 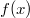 an einer bestimmten Stelle lässt sich mithilfe der Tangente 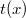 an dieser Stelle veranschaulichen. Die Tangente ist eine Gerade, die den Funktions graphen in einem Punkt berührt und in der Umgebung dieses Punktes approximiert. Daher kann man hiermit die Steigung leicht berechnen, z. B. mit einem Steigungsdreieck. Nicht differenzierbare FunktionenEs gibt Funktionen, bei denen sich an bestimmten Stellen die Steigung nicht bestimmen lässt. Die folgende Grafik zeigt eine solche Funktion: Im Minimum der fett gezeichneten Funktion (es ist eine Betragsfunktion, nämlich 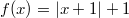 ), also im Punkt 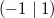 , lässt sich keine Tangente finden. Hier sind zur Illustration drei Geraden mit unterschiedlicher Steigung eingezeichnet. Es existieren unendlich viele Geraden, die den Funktionsgraphen in diesem Punkt berühren, ohne dass eine besser oder schlechter wäre als die anderen. Entsprechend kann in diesem Punkt keine Steigung der Funktion bestimmt werden. Man sagt: Die Funktion ist im Punkt 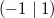 nicht differenzierbar nicht differenzierbar. AbleitungsregelnFür die Berechnung von Ableitungsfunktionen gibt es verschiedene Regeln. Dabei sind 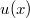 , 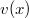 , 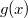 und 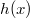 Funktionen, aus denen 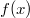 zusammengesetzt ist. Bei der Quotientenregel muss 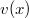 immer ungleich 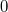 sein. Konstantenregel: Für 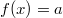 , 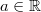 ,  konstant, ist 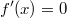 Faktorregel: Faktorregel: Für 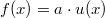 , 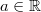 ist 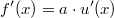 Potenzregel: Potenzregel: Für 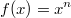 , 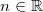 ist 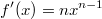 Summenregel: Summenregel: Für 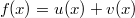 ist 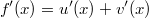 Produktregel: Produktregel: Für 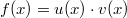 ist 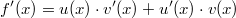 Quotientenregel: Quotientenregel: Für 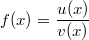 ist 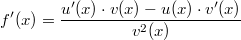 Kettenregel: Kettenregel: Für 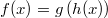 ist 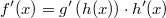 Bemerkung 1: Bemerkung 1: Bei komplizierteren Funktionen müssen diese Regeln kombiniert angewendet werden. Bemerkung 2: Da die Summenregel deutlich einfacher ist als die Produktregel, erleichtert es das Ableiten, wenn eine Funktion möglichst weit ausmultipliziert vorliegt. Bemerkung 3: Häufig können auch die Potenzgesetze helfen, z. B. gilt 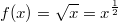 . Daher ist 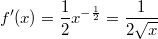 . Wer diesen Weg kennt, muss wesentlich weniger Ableitungsregeln auswendig kennen. Ableitungen von weiteren FunktionenNatürlich können auch trigonometrische sowie Exponential- und Logarithmusfunktionen abgeleitet werden. Ihre Ableitungen werden meist unter der Überschrift "Spezielle Ableitungen" zusammengefasst. Achtung: Bitte achten Sie jeweils auf die Definitionsbereiche sowie mögliche Einschränkungen für Parameter (siehe die entsprechenden Kapitel)! Sinusfunktion: Für 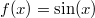 ist 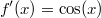 Kosinusfunktion: Kosinusfunktion: Für 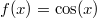 ist 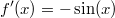 Tangensfunktion: Tangensfunktion: Für 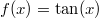 ist 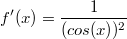 Exponentialfunktion 1: Exponentialfunktion 1: Für 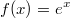 ist 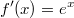 Exponentialfunktion 2: Exponentialfunktion 2: Für 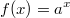 ist 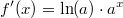 Logarithmusfunktion: Logarithmusfunktion: Für 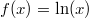 ist 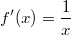 Zur Berechnung von ExtremstellenHat eine Funktion eine Extremstelle, bietet sich zur Berechnung dieser Stelle häufig das folgenden Verfahren an: Notwendige Bedingung: Hat 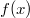 in 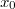 eine Extremstelle, ist 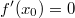 Hinreichende Bedingung: Hinreichende Bedingung: Lässt sich eine Funktion 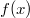 zweimal ableiten und gilt sowohl 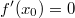 als auch 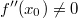 , so hat 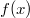 im Punkt 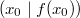 ein lokales Extremum. Ist 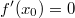 und 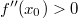 , handelt es sich um ein lokales Minimum. Ist 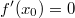 und 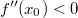 , handelt es sich um ein lokales Maximum. Bemerkung: Es gibt Extremstellen, z. B. an den Rändern des Definitionsbereichs oder an Stellen, an denen keine Steigung bestimmt werden kann (siehe oben), die mithilfe dieses Verfahrens nicht gefunden werden können. Weitere Informationen zum Thema |
|
 Brückenkurs
Brückenkurs