Erklärungen
Mathematischer
Hinweis vorab: Wie schon der Begriff
"Ableitung" würde die Betrachtung von Integralen die
Verwendung von Grenzwerten erfordern. Darauf wird im
Rahmen diese Brückenkurses aber verzichtet, da hier
der Umgang mit und das Berechnen von (einfachen)
Integralen im Mittelpunkt stehen und ein grobes
Verständnis der Hintergründe dafür erstmal ausreicht.
Organisatorischer
Hinweis vorab: Natürlich werden in diesem
Kapitel auch Beispiele durchgerechnet. Sie finden
diese am Ende des Kapitels und nicht zwischendurch wie
bei anderen Themen, da hier erst relativ viel Theorie
bekannt sein muss, damit die Beispiele verstanden
werden können.
Integrieren als
Umkehrung des Differenzierens
Zunächst ein paar
"Vokabeln":
Die Berechnung von Integralen nennt man Integration.
In 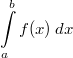
(gesprochen: "Integral von a bis b über f von x dx"
oder "Integral von a bis b über f von x nach dx")
heißt / heißen
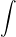 das Integralzeichen. das Integralzeichen.- die
Zahlen
 und
und  Integrationsgrenzen.
Genauer: Integrationsgrenzen.
Genauer:  ist die untere Integrationgrenze,
ist die untere Integrationgrenze,  die obere. In unserem Fall handelt es sich um reelle
Zahlen, später können die
Integrationsgrenzen auch aus anderen
Zahlenbereichen stammen.
die obere. In unserem Fall handelt es sich um reelle
Zahlen, später können die
Integrationsgrenzen auch aus anderen
Zahlenbereichen stammen.
- die zu
integrierende Funktion
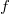 Integrand. Integrand.
- die Variable
 Integrationsvariable.
Ist (wie hier) die Integrationsvariable Integrationsvariable.
Ist (wie hier) die Integrationsvariable  , spricht man auch
von der Integration über , spricht man auch
von der Integration über  .
Natürlich kann man statt .
Natürlich kann man statt  auch andere Integrationsvariablen verwenden. Man
sollte dann nur aufpassen, dass der Name nicht
schon an andere Stelle (z. B. bei den
Integrationsgrenzen) verwendet wird. Sonst wird
die ganze Sache mehrdeutig...
auch andere Integrationsvariablen verwenden. Man
sollte dann nur aufpassen, dass der Name nicht
schon an andere Stelle (z. B. bei den
Integrationsgrenzen) verwendet wird. Sonst wird
die ganze Sache mehrdeutig...
- das
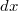 Differential.
Mit diesem Begriff muss man ein bisschen
vorsichtig sein, da er auch in anderen Kontexten
und z. T. mit anderer Bedeutung verwendet wird. In
diesem Zusammenhang ist es ein symbolischer
Bestandteil der Notation, der angibt, über welche
Variable integriert wird. Dies ist z. B. dann
wichtig, wenn Parameter
in der Funktionsgleichung enthalten sind. Differential.
Mit diesem Begriff muss man ein bisschen
vorsichtig sein, da er auch in anderen Kontexten
und z. T. mit anderer Bedeutung verwendet wird. In
diesem Zusammenhang ist es ein symbolischer
Bestandteil der Notation, der angibt, über welche
Variable integriert wird. Dies ist z. B. dann
wichtig, wenn Parameter
in der Funktionsgleichung enthalten sind.
Wichtig:
Jede auf einem abgeschlossenen
Intervall ![[a \; ; \; b]](./teximg/img1645.png) stetige
stetige
Funktion ist integrierbar.
Der Begriff " Stetigkeit"
wurde im Rahmen dieses Brückenkurses nicht weiter
definiert. Für uns reicht hier das
"Alltagsverständnis" von Stetigkeit, nämlich dass die
Funktion ohne abzusetzen von 
bis 
durchgezeichnet werden kann. Sie darf (sehr
unmathematisch formuliert) also keine Unterbrechungen,
Lücken, Sprünge o. ä. haben. "Knicke" wie bei der Betragsfunktion
sind hingegen kein Problem. Zusätzlich ist wichtig,
dass es sich um ein abgeschlossenes Intervall handelt;
offene oder
halboffene
Intervalle sind hier nicht möglich.
Allerdings ist die Berechnung von Integralen - im
Gegensatz zum Ableiten -
auch schon bei relativ einfachen Funktionen nicht immer elementar
möglich - und selbst wenn, ist sie nicht
immer einfach, u.a. weil kein allgemeingültiger
Algorithmus, also kein "Rezept", dafür existiert. Um
Integrale zu bestimmen, muss man aus einer Vielzahl
von möglichen Wegen den finden, der zum Ziel führt.
Mögliche Wege sind die Anwendung der
Integrationsregeln (Ähnliches kennt man vom Ableiten),
Rückführen der gesuchten Integrale auf Grundintegrale,
Nachschlagen in Integraltafeln oder die Nutzung
spezieller Software. Häufig hilft trotzdem nur
geschicktes Raten oder eine auf der ersten Blick eher
abwegige Idee. Daher gilt: Mehr noch als bei anderen
Themen ist hier viel, viel Üben nötig...
Das unbestimmte
Integral - Was ist das?
Definition:
Gilt 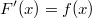
, so ist 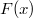
eine Stammfunktion
der Funktion 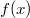
Die Formulierung " eine
Stammfunktion" deutet schon darauf hin, dass es zu
einer Funktion viele Stammfunktionen gibt. Die Menge
aller Stammfunktionen nennt man unbestimmtes Integral
der Funktion 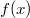
und schreibt 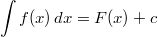
mit der Konstanten
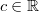
 ist die
sogenannte Integrationskonstante.
Sie ist deswegen wichtig, weil zwei Funktionen, die
sich nur um eine additive
Konstante unterscheiden, die gleiche Ableitung
haben. Anders formuliert: Beim Ableiten fällt die
Konstante weg. Bei der Umkehrung des Ableitens kann
dann nicht mehr ohne Weiteres bestimmt werden, welche
Konstante in der Ursprungsfunktion möglicherweise
enthalten war. Da die Konstante in inhaltlichen
Zusammenhängen aber wichtig werden kann, darf man sie
nicht einfach "unter den Tisch fallen lassen". Also
nimmt man eine allgemeine Konstante 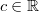 Ganz
wichtig:
Ganz
wichtig: Die Stammfunktion / das unbestimmte
Integral einer Funktion ist wieder eine Funktion bzw.
eine Menge von Funktionen!
Bemerkung:
So wie man die Ableitung
einer Funktion mit einen hochgestellten Strich an der
Funktionsbezeichnung kennzeichnet (die Ableitung von 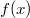 heißt i. A. 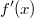 ), nennt man
Stammfunktionen üblicherweise 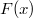
(gesprochen: "groß f von x"), wenn die Funktion 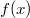 heißt. Hält
man sich an diese Konvention, wird bereits durch die
Bezeichnungen deutlich, in welchem Verhältnis die
Funktionen zueinander stehen.
Das bestimmte
Integral - Was ist das?
Die
Integralrechnung kann dazu genutzt werden, Flächen zu
berechnen. Das ist ja wahrscheinlich genau das, woran
die Meisten denken, wenn sie das Wort "Integral"
hören. Die Bedeutung der Integralrechnung geht aber
weit über diesen Bereich hinaus. Bleibt man bei der
Flächenberechnung, kann man noch etwas genauer sagen:
Man verwendet die Integralrechnung, um krummlinig begrenzte
Flächen (in unserem Fall: der Ebene) zu
berechnen. Gradlinig begrenzte Flächen der Ebene, z.
B. von Quadraten, Rauten oder Dreiecken, können
mithilfe der Geometrie
bestimmt werden. Bei einigen krummlinig begrenzten
Flächen, wie vom Kreis oder von Kreissegmenten,
funktioniert dies auch so. Werden die Flächen
komplizierter, gibt es keine geschlossenen Formeln
mehr, sodass die Integralrechnung zum Zuge kommt.
Im Unterschied zum "geometrischen" Weg liefert die
Integralrechnung einen sogenannten orientierten
Flächeninhalt. Das bedeutet, dass Flächen,
die unterhalb der x-Achse liegen, negativ zählen. Das
bestimmte Integral gibt also nicht direkt den
Flächeninhalt zwischen der Funktion und der x-Achse
bezogen auf ein bestimmtes, abgeschlossenes Intervall
an, sondern ein Art Flächenbilanz, also die Summe aus
den positiv gezählten Flächeninhalten oberhalb der
x-Achse und den negativ gezählten Flächeninhalten
unterhalb der x-Achse. Geschrieben wird dies: 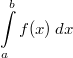
Man berechnet ein solches bestimmtes Integral, indem
man eine Stammfunktion 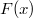
von 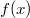
berechnet und die Differenz 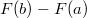
bildet. Man schreibt: ![\int \limits_a^bf(x) \, dx = \left[ F(x) \right]_a^b = F(b)-F(a)](./teximg/img1655.png) Merksatz:
Merksatz:
"Funktionswert von 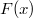
an der oberen Grenze minus Funktionswert von 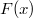 an der unteren Grenze"
Dieser Zusammenhang beruht auf einem der wichtigsten
Sätze zu diesem Thema, nämlich dem Fundamentalsatz der
Analysis, auch Hauptsatz der
Differenzial- und Integralrechnung genannt.
Ganz
wichtig: Das bestimmte Integral einer
Funktion ist eine Zahl!
Einige
Eigenschaften des bestimmten Integrals
- Sind die
obere und die untere Integrationsgrenze identisch,
hat das bestimmte Integral den Wert
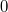 : : 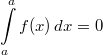
- Das
bestimmte Integral über das ganze Intervall ist
gleich der Summe der bestimmten Integrale über
Teilintervalle (Achten Sie auf die
Integrationsgrenzen!):
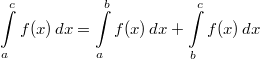
- Ist im
ganzen Integrationsintervall
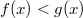 , so gilt , so gilt 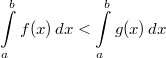
- Vertauscht
man die Integrationsgrenzen, wechselt das
bestimmte Integral das Vorzeichen:
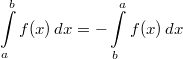
Grund- oder
Stammintegrale
Als Grund- oder
Stammintegrale bezeichnet man die (unbestimmten)
Integrale einiger häufig vorkommender Funktionen.
Bitte beachten Sie jeweils die Definitionsbereiche
der Funktionen sowie ggf. nötige Einschränkungen!
Die Integrationskonstante sei 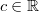 Ganz rationale
Funktionen
Für ganz
rationale Funktionen gilt
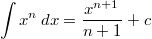
mit 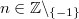 Bemerkung:
Bemerkung:
Die Integrationsregel ist hier nur für eine sehr
einfache ganz rationale Funktion, auch Potenzfunktion
genannt, aufgeführt. Mithilfe der Summen- und
Faktorregel (siehe unten) funktioniert diese Regel
auch für allgemeine ganz rationale Funktionen.
Mithilfe der Potenzgesetze
kann diese Regel auch für Wurzelfunktionen
und einfache gebrochen
rationale Funktionen angewendet werden und gilt
nämlich:
![\int \sqrt[n]{x} \, dx = \int x^\frac{1}{n} \, dx = \frac{x^{\frac{1}{n}+1}}{\frac{1}{n}+1} = \frac{n}{n+1}x^\frac{1+n}{n}+c](./teximg/img1664.png)
und
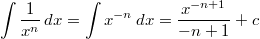 Achtung:
Achtung:
Diese Regel gilt nicht, wenn der
Exponent 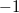 ist, also für
die Funktion 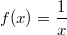
, da 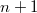 in
diesem Fall nämlich 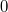
ist und durch 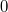
bekanntermaßen nicht geteilt werden darf. Hier gilt
(etwas überraschend):
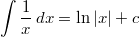 Bemerkung:
Bemerkung:
Dies ist ein gutes Beispiel dafür, dass sich Integrale
manchmal anders "verhalten", als man hätte denken
können, und damit, warum hier viel Übung und Erfahrung
nötig ist. Der Gedanke, dass das Integral einer ganz
rationalen Funktion wieder ein ganz rationale Funktion
ist, ist ja durchaus nicht abwegig. In den meisten
Fällen stimmt das auch - aber eben nicht immer... Exponential- und
Logarithmusfunktionen
Trigonometrische
Funktionen
Integrationsregeln
und -methoden
Bei einer
komplexeren Funktion gibt es zwei Ansätze: Entweder
die Funktion lässt sich durch geeignete Umformungen
auf eines der Grundintegral zurückführen oder man
versucht mithilfe der hier aufgezeigten
Integrationsmethoden weiterzukommen. Allerdings gibt
es (wie oben schon gesagt) auch Funktionen, die sich
nicht "vernünftig" integrieren lassen.
Zunächst zwei Regeln, deren Pendants Sie schon bei den
Ableitungsregeln
kennengelernt haben. Faktorregel
Enthält der
Integrand einen konstanten
Faktor 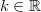 , so
kann dieser vor das Integral gezogen werden: 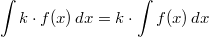 Summenregel
Das Integral einer
Summe
zweier Funktionen
ist gleich der Summe der Integrale der beiden
Funktionen: 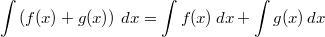
Bemerkung: Das gilt natürlich auch für Summen
mit mehr als zwei Summanden.
Sozusagen die Umkehrung der Produktregel
für das Ableiten ist die Partielle Integration
für unbestimmte
Integrale: 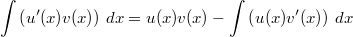
für bestimmte Integrale: ![\int\limits_a^b \left(u'(x)v(x)\right) \, dx = \left[u(x)v(x)\right]_a^b-\int\limits_a^b \left(u(x)v'(x)\right) \, dx](./teximg/img1680.png)
Auch die Kettenregel
hat hier eine Entsprechung, nämlich die Integration durch
Substitution
für unbestimmte
Integrale: 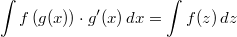 mit 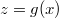
und 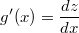
alternativ: 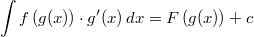
für bestimmte Integrale: 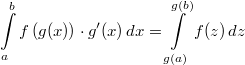 mit 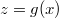
und 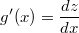
Ein Sonderfall der Integration durch Substitution ist
die Logarithmische
Integration
Beispiele
Berechnung eines
bestimmten Integrals
Gesucht sei 
Nach der Formel für das Integral von ganz rationalen
Funktionen und der Faktorregel gilt
![\begin{array}{rcl} \int\limits_0^3 2x \, dx &=& 2\int\limits_0^3 x^1 \, dx \\ &=& 2\cdot\left[\frac{x^2}{2}\right]_0^3 \\&=& 2\left(\frac{3^2}{2}-\frac{0^2}{2}\right) \\ &=& 2\cdot \frac{9}{2} \\ &=& 9 \end{array}](./teximg/img1690.png) Bemerkung:
Bemerkung:
Man kann sich fragen, warum diese Rechnung kein  enthält.
Korrekterweise ist ja 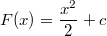 . Hier die Rechnung mit
 :
![\begin{array}{rcl} \int\limits_0^3 2x \, dx &=& 2\cdot\left[\frac{x^2}{2}+c\right]_0^3 \\&=& 2\left(\left(\frac{3^2}{2}+c\right)-\left(\frac{0^2}{2}+c\right)\right) \\ &=& 2\left(\frac{9}{2}+c-0-c\right) \\ &=& 9 \end{array}](./teximg/img1692.png)
Man stellt fest, dass sich das 
während der Rechnung aufhebt. Daher wird es in diesem
Zusammenhang meist gleich weggelassen.
Alternativer
Weg: Zeichnet man die Funktion in ein Koordinatensystem,
erkennt man, dass die schraffierte Fläche 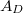 die Form eines Dreiecks
hat: Die Fläche
eines Dreiecks lässt sich aber auch ohne
Integralrechnung bestimmen, nämlich
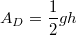
mit 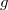 :
Grundseite und 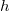 :
Höhe auf die Grundseite
In diesem Fall ist 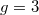
und 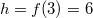 .
Daraus ergibt sich 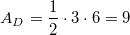
Das ist natürlich kein Beweis dafür, dass die Regel
für die Integration von ganz rationalen Funktionen
richtig ist (Es hätte uns aber schon verwundern
müssen, wenn etwas anderes herausgekommen wäre...).
Dies soll nur als kleine Plausibilisierung der Regel
dienen sowie als Erinnerung, dass es häufig nicht nur
einen Lösungsweg gibt. Berechnung von
Flächeninhalten
Soll anstelle des
bestimmten Integrals der Flächeninhalt bestimmt
werden, der vom Graphen und der x-Achse in einem
bestimmten Intervall eingeschlossen wird, muss man die
Funktion vor dem Integrieren ein bisschen genauer
anschauen. Hat die Funktion in dem Intervall nämlich
Nullstellen (d. h. liegen Teile der zu berechnenden
Fläche unterhalb und andere Teile oberhalb der
x-Achse), unterscheidet sich der Wert des Integrals
von der Größe des Flächeninhalts, weil die Flächen
unterhalb der x-Achse ja negativ in den Wert Integrals
einfließen. Bei der Berechnung der Fläche als solche
zählen sie aber natürlich positiv.
Einfaches
Beispiel
Gesucht sei die Fläche, die von der x-Achse und der
Funktion 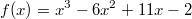
im Intervall ![[1\;;\;4]](./teximg/img1701.png)
eingeschlossen wird. Sie ist in der folgenden Grafik
schraffiert eingezeichnet. Die Grafik zeigt:
Die Funktionswerte sind im gesamten betrachteten
Intervall größer als 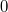
. Das bedeutet, dass die Größe des Flächeninhaltes und
der Wert des bestimmten Integrals 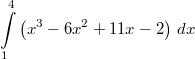 gleich sind. Es gibt ja
keine Flächen unterhalb der x-Achse, die negativ
gezählt werden könnten.
Nach der Formel für das Integral von ganz rationalen
Funktionen und die Summen- und Faktorregel gilt
![\begin{array}{rcl} \int\limits_1^4 \left(x^3-6x^2+11x-2\right)\,dx &=& \int\limits_1^4 x^3 \, dx +\int\limits_1^4 -6x^2\,dx+\int\limits_1^4 11x\, dx +\int\limits_1^4 -2\,dx \\ &=& \int\limits_1^4 x^3 \, dx -6\int\limits_1^4 x^2\,dx+11\int\limits_1^4 x\, dx -2\int\limits_1^4 1\,dx \\ &=& \left[\frac{1}{4}x^4-6\cdot\frac{1}{3}x^3+11\cdot\frac{1}{2}x^2-2x\right]_1^4\\ &=& \left[\frac{1}{4}x^4-2x^3+\frac{11}{2}x^2-2x\right]_1^4 \\ &=& \frac{1}{4}\cdot4^4-2\cdot4^3+\frac{11}{2}\cdot4^2-2\cdot4-\left(\frac{1}{4}-2+\frac{11}{2}-2\right) \\ &=& \frac{57}{4} \end{array}](./teximg/img1703.png)
Die Fläche 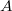
ist also 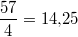
Flächeneinheiten groß.
Bemerkung:
So ausführlich wie in dieser Beispielrechnung wird man
den Lösungweg sonst nicht aufschreiben...
Etwas
schwierigeres Beispiel
Gesucht sei die Fläche, die von der x-Achse und der
Funktion 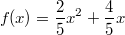 im Intervall ![[-2\;;\;1]](./teximg/img1707.png) eingeschlossen wird. In
der folgenden Grafik sieht man, dass die Gesamtfläche
(schraffiert) in zwei Teilflächen 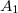
und 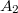
zerfällt. Um die Größe der
gesamten eingeschlossenen Fläche zu berechnen, muss
nun also das Integral an der im Intervall ![[-2\;;\;1]](./teximg/img1707.png) liegenden Nullstelle
aufgeteilt werden. Dann werden die Einzelflächen
berechnet und anschließend deren Beträge addiert.
Nullstellen berechnen
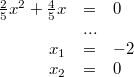
Da nur die zweite Nullstelle tatsächlich innerhalb der
betrachteten Intevalls liegt, ist nur sie gerade
interessant.
Zu berechnen ist nun also
![\begin{array}{rcl} A_1 &=& \int\limits_{-2}^0 \left(\frac{2}{5}x^2+\frac{4}{5}x\right)\,dx \\ &=& \left[\frac{2}{5\cdot 3}x^3+\frac{4}{5\cdot 2}x^2\right]_{-2}^0 \\ &=& \frac{2}{15}\cdot 0+\frac{2}{5}\cdot 0-\left(\frac{2}{15}\cdot\left(-2\right)^3+\frac{2}{5}\cdot\left(-2\right)^2\right) \\ &=& -\frac{8}{15} \end{array}](./teximg/img1711.png)
![\begin{array}{rcl} A_2 &=& \int\limits_{0}^1 \left(\frac{2}{5}x^2+\frac{4}{5}x\right)\,dx \\ &=& \left[\frac{2}{5\cdot 3}x^3+\frac{4}{5\cdot 2}x^2\right]_0^1 \\ &=& \frac{2}{15}\cdot 1+\frac{2}{5}\cdot 1-0 \\ &=& \frac{8}{15} \end{array}](./teximg/img1712.png)
Das ergibt für die Gesamtfläche 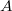
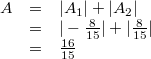 Bemerkung:
Bemerkung:
Man sieht hier sehr schön, was passieren würde, wenn
man die Nullstelle oder die Betragsstriche in der
Rechnung ignorieren würde. Für 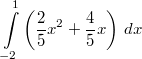 ergäbe sich nämlich 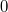 , was sicherlich
nicht die Größe der schraffierten Fläche ist. Anwendung der
Partiellen Integration
Gesucht sei 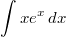 mit 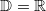
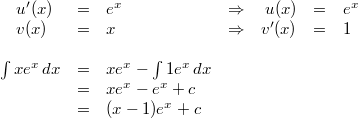
mit 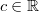 Bemerkung
1:
Bemerkung
1: Die Partielle Integration lohnt sich immer
dann, wenn ein Faktor
einfach(er) integriert werden kann und das Integral
auf der rechten Seite gut zu lösen ist. Deswegen wurde
hier 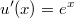
gesetzt, weil 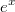
unkompliziert zu integrieren ist. Außerdem vereinfacht
sich das Integral auf der rechten Seite, da beim
Ableiten von 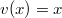
nur eine 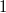
stehenbleibt.
Bemerkung
2: Bei der vorletzten Umformung wäre es auch
möglich
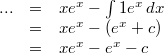
zu schreiben. Da 
aber ohnehin eine beliebige reelle Zahl ist, kommt es
auf das Vorzeichen hier nicht an. Anwendung der
Integration durch Substitution
Gesucht sei 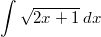 mit 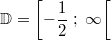
Substitutieren wir 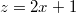 ,
ist die Ableitung davon 
. Durch die Substitution wird nun 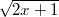 zu 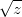 . Wenn wir nach  integrieren wollen, muss
am Ende des Integrals auch 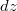
(und nicht 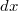 )
stehen. 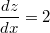
lässt sich umformen zu 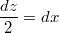 .
Aus unserem Integral wird also:
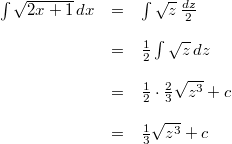
Nun kommt noch die Rücksubstitution, denn die
eigentlich Aufgabe war ja das Integral mit der
Integrationsvariable 
zu lösen:
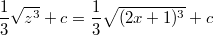 Bemerkung
1:
Bemerkung
1: Ziel der Substitution ist es, den
Integranden zu vereinfachen. Dazu kann es manchmal
nötig sein, eine Substitution zu verwenden, die auf
den ersten Blick komplizierter ist.
Bemerkung
2: In diesem Beispiel wurde "nur" ein
Spezialfall der Integration durch Substitution
gezeigt, nämlich die lineare Substitution. An ihr
lässt sich das Prinzip gut verdeutlichen, weil sie ein
gutes Stück einfacher ist als Substitutionen im
Allgemeinen.
Bemerkung
3: 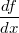
ist eine andere Schreibweise für 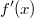
. Da das  ,
mit dem wir substituieren, von 
abhängt, können wir 
auch nach 
ableiten und das ganze als 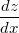
schreiben.
Bemerkung
4: Die Integration durch Substitution wird
immer dann angewendet, wenn ein Faktor des Integranden
die Ableitung der inneren Funktion des anderen Faktors
ist. Als Faustregel kann gesagt werden: Substitution
ist beim Integrieren immer dann angezeigt, wenn man
die Kettenregel
benutzen würde, um den Term
abzuleiten.
|
 Brückenkurs
Brückenkurs