Wie Sie feststellen können, wird es mit fortschreitender Zeit immer schwieriger,den Verlauf der Infektion mit einer Exponentialfunktion zu modellieren - wenn Sie eine Funktion finden, die das Verhalten in den ersten Tagen gut annähert, so liegt die Zahl der Infizierten in China seit Ende Januar deutlich unter der Zahl, die sich aus dieser Funktion ergibt., das im Januar noch gut gepasst hat.
Es gibt offenbar neue Faktoren, die die Ausbreitung der Infektion hemmen. Dies macht es erforderlich, das verwendete Modell anzupassen um die Qualität der Hochrechnungen zu verbessern,
Ehe wir nach neuen Modellen suchen, wollen wir zunächst analysieren, wie gut eine Exponentialfunktion für die Modellierung der Infektionszahlen geeignet ist. Eine solche Funktion hat die Form $a\cdot e^{kx}$. Der Wert $a$ ist dabei leicht zu bestimmen - es ist der Wert für $x=0$, also $a=278$.
Der Koeffizient $k$ bestimmt, wie schnell die Kurve ansteigt. Wenn wir die Zahl der Infektionen am Tag $n$ mit $i_n$ bezeichnen, so its $a=i_0$ und $i_n=a\cdot e^{kn}=i_0\cdot e^{kn}$ - natürlich nur unter der Annahme, dass die Zahl der Infektionen wirklich durch eine Exponentialfunktion beschrieben werden kann. Dann könnte man $k$ für $n > 0$ berechnen als $k=\frac{\ln i_n - \ln i_0}{n}$.
Natürlich unterliegt die Zahl der Infektionen zufälligen Schwankungen, so dass damit zu rechnen ist, dass sich für jeden Tag ein anderer Wert für $k$ ergibt - bezeichnen wir den Wert für den Tag $n$ mit $k_n=\frac{\ln i_n - \ln i_0}{n}$. Je mehr fie Folge $k_n$ von einer konstanten Folge abweicht, desto schlechter wird das Infektionsverhalten durch eine Exponentialfunktion beschrieben. Wie stark schwnkt dieser Wert? Dies zeigt das folgende Diagramm.
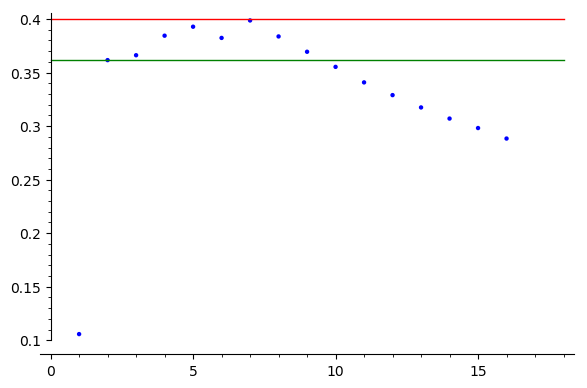
Der Wert $k_1$ für Tag 1 ist offenbar ein "Ausreißer". Um ihn zu erklären müsste man die Erfassung der Daten genauer kennen. Danach bewegt sich der Parameter $k$ in einem Korridor mit einer Breite von $0.04$ aus dem er am Tag 10 ($n=10$, 31.1.2020) ausbricht. Von diesem Tag an sollten wir unser Modell korrigieren.